Matematické Fórum

nanny1 · 28. 01. 2014 10:58 — Editoval nanny1 (28. 01. 2014 12:13)

Ahoj, prosím o radu, nejsem si jistá, jestli to chápu dobře. Zadání:
//forum.matweb.cz/upload3/img/2014-01/01451_souradnice.png
Výpočet obou bází je mi jasný, bod B, který je obrazem bodu A má teda souřadnice [-1,1]. Bázové vektory sdružené báze (s horními indexy) budou tečnami ke křivkám, což je v tomhle případě parabola a přímka, v bodě B. Je to tak? A teď si nejsem úplně jistá, jestli jsem správně nakreslila tu parabolu a bázové vektory.. Křivka q1 v soustavě $r^{i}$ je přímka rovnoběžná s osou r1 a procházející bodem B, křivka q2 je parabola, která má počátek v bodě B a vypadá jako klasická parabola $y=x^{2}$ . Tečné vektory - báze vycházejí $\vec{e}^{1}=(1,0),\vec{e}^{2}=(0,0.5)$ , ale do obrázku nesedí.

Brano · 29. 01. 2014 15:11 — Editoval Brano (29. 01. 2014 22:54)

podla mna by to malo byt takto:

$r^1=q^1-2q^2$ a $r^2=(q^2)^2$ - teda
$dr^1=dq^1-2dq^2$ a $dr^2=2q^2dq^2$ cize v bode $(q^1,q^2)=(1,1)$ je to $dr^2=2dq^2$ co v tvojom znaceni zodpoveda

kovariantna baza: $e^1=(1,-2)$ a $e^2=(0,2)$ a kontravariantnu bazu dostaneme ak invertujeme zodpovedajucu maticu - t.j.
$\begin{pmatrix}1&-2\\0&2\end{pmatrix}^{-1}=\begin{pmatrix}1&1\\0&1/2\end{pmatrix}$ teda
kovariantna baza: $e_1=(1,0)^T$ a $e_2=(1,1/2)^T$ .

EDIT: zle som predtym odcital bazu z matice - teraz je to snad ok.

PS: ale dlho som sa geometrii nevenoval, tak mozem uz mat popletene co je kovariantny a co kontravariantny

resp. este som si uvedomil, ze mi zo zadania nie je uplne jasne, ci sa tym mysli bazu "r-iek" v priestore "q-ciek" alebo naopak - ja som robil to prve.

grizzlybear · 31. 01. 2014 16:15

Přispěju obrázkem. Pokud uděláme pravoúhlou soustavu r1 (doprava) a r2 (nahoru), pak pokd zafixujeme q1=K dostaneme rovnice:

r2=(r1-K)^2 / 4
tj. parabolu, co prochází B(-1,1) s vrcholem (0,1/4) (K=1).
Druhá křivka vzniklá zafixováním q2=L je r2=L, r1=Q1-2L. Tj. přímka rovnoběžná s r1. Ne tolik formální cestou pak vyjdou složky báze tečné k právě jmenovaným křivkám. Pro q2- konst je to (1,0) vůči bázi r2 a r1.
A pro tečnu k parabole- klasickou derivací- 2r1/4. To v bodě r1=-1 dá -1/2. Vektor je potom (1, -1/2). Tyto vektory mohou být násobeny nenulovou konstantou => různost výsledků. Mě tento výsledek odpovídá Branově kovariantní bázi.

Jinak si myslím, že se to prakticky dělá přes Jakobián (ten dá asi i jednoznačnou velikost vektorů)- ale zas tak dobře tomu nerozumím. Plus se mi taky plete, co je ko- a co kontra.

Brano · 31. 01. 2014 18:46 — Editoval Brano (31. 01. 2014 18:50)

↑ grizzlybear:
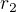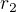To ze mame rozne vysledky je presne kvoli tomu co som pisal uplne na konci - tie vektory ako mam ja by ti vysli, keby si najprv fixoval $r_2$ a hybal s $r_1$ - a nakreslil to v rovine $q_1q_2$ a potom fixoval $r_1$ a hybal s $r_2$ - zatial co ty si fixoval 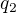$q_2$ a hybal s $q_1$ - a nakreslil to v rovine $r_1r_2$ a potom fixoval $q_1$ a hybal s $q_2$ .

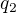No a to co sa mne zo zadania nezda uplne jasne je to, ze ci sa tym mysli to co som to robil ja, alebo to co si to robil ty - lebo to su dve v podstate rozne veci.

nanny1 · 31. 01. 2014 19:11 — Editoval nanny1 (31. 01. 2014 22:32)

↑ grizzlybear: ↑ Brano: Děkuju moc oběma, už si to dokážu představit. Parabolu jsem měla nakreslenou jinde a udělala jsem početní chybu při určování inverzní matice zobrazení, proto to nevycházelo. Taky se mi to plete, teoreticky to vím - kontravariantní je původní křivočará a kovariantní je k ní sdružená, ale jak dojde na kreslení, mám v tom trochu hokej, kam co nakreslit. Naštěstí jsem kreslení u zkoušky nechytla, za což jsem ráda, protože tohle mi zabere ještě nějaký čas, než se mi to rozleží.

Matematické Fórum

#1 28. 01. 2014 10:58 — Editoval nanny1 (28. 01. 2014 12:13)

Transformace souřadnic

#2 29. 01. 2014 15:11 — Editoval Brano (29. 01. 2014 22:54)

Re: Transformace souřadnic

#3 31. 01. 2014 16:15

Re: Transformace souřadnic

#4 31. 01. 2014 18:46 — Editoval Brano (31. 01. 2014 18:50)

Re: Transformace souřadnic

#5 31. 01. 2014 19:11 — Editoval nanny1 (31. 01. 2014 22:32)

Re: Transformace souřadnic

Zápatí