Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 02. 2014 17:04 — Editoval Mirgeee (16. 02. 2014 17:05)
Potenciál nabité destičky
Dobrý den, mám problém s další úlohou z elektrostatiky...
Určete potenciál ve středu destičky nabité nábojem Q, má li destička tvar čtverce o straně a.
Myslím, že to lze řešit tak, že bych si zjistil potenciál ve vzdálenosti x od prostředku tenké tyče délky a. Ten vychází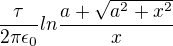 .
.
Kdybych integroval ten od -a/2 do a/2, dostal bych správný výsledek? Ten integrál vypadá dost děsivě, nejde to řešit jednodušeji?
Díky za pomoc...
Offline
#2 16. 02. 2014 17:57
Re: Potenciál nabité destičky
↑ Mirgeee:
Dobrý den, těmto věcem až tak nehovím, ale řekl bych, že pro integraci bude lepší nevycházet z pevné délky tenké tyče. Účelnější bude rozdělit čtverec úhlopříčkami na 4 trojúhelníky a integrovat přes tyto samostatné segmenty. Pak bude délka tenké tyče 'a' úměrná vzdálenosti x od středu - čili proměnná x se ve výrazu vykrátí a integrace se podstatně zjednodušší. Myslím, že jsem na tento postup už někde narazil.
Pokud se tedy nemýlím.
Offline
#3 16. 02. 2014 20:36
Re: Potenciál nabité destičky
↑ Mirgeee:
Ahoj
Podle mě máš ale špatně ten vzorec co uvádíš.![kopírovat do textarea $\varphi (x)=\frac{\tau }{4\pi \varepsilon _{0}}\int_{-a}^{a}\frac{dy}{\sqrt{x^{2}+y^{2}}}=\frac{\tau }{4\pi \varepsilon _{0}}[ln(\frac{y}{x}+\sqrt{1+\frac{y^{2}}{x^{2}}}]_{-a}^{a}$](/mathtex/f1/f181b10f4f4f1c7822af8426f32e0086.gif)
což se nerovná tomu co píšeš ty
Offline
#4 17. 02. 2014 16:53
Re: Potenciál nabité destičky
↑ Brzls:
Zdravím, řekl bych, že se výsledek ještě dá upravit: ![kopírovat do textarea $\frac{\tau }{4\pi \varepsilon _{0}}[ln(\frac{y}{x}+\sqrt{1+\frac{y^{2}}{x^{2}}}]_{-a}^{a}=\frac{\tau }{4\pi \varepsilon _0}[ln\frac{y+\sqrt{x^2+y^2}}{x}]_{-a}^{a}=$](/mathtex/aa/aa3df8b18701589e8deb874d3e2ef968.gif)
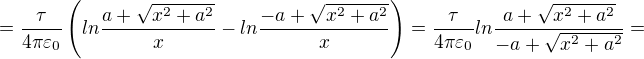
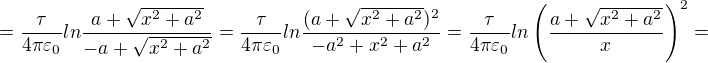

Jen bych řekl (s ohledem na meze integrace od -a do a), že vzorec není pro délku tyče a, jak píše kolega ↑ Mirgeee:, ale pro délku 2a.
Pokud se tedy nemýlím.
Offline
#5 17. 02. 2014 18:23
Re: Potenciál nabité destičky
↑ Jj:
Omlovám se nějak mi ta úprava nedošla, počítal sem to rovnou potom pro tu destičku, s tim postupem co jste navrhoval to rovnou přecházelo na jednoduchý výsledek, takže sem nad tou úpravou moc nepřemýšlel
Offline
