Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 08. 03. 2014 17:08
- janca361

- .
- Příspěvky: 3284
Re: Tečny k elipse
↑ Sheldon.C:
Urči průsečíky přímky a elipsy. Potom hledáš vzdálenost průsečíků.
Offline
#4 08. 03. 2014 17:26
- janca361

- .
- Příspěvky: 3284
Re: Tečny k elipse
↑ Sheldon.C:
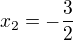
To máš správně, ale  máš špatně dopočítané (u bodu B).
máš špatně dopočítané (u bodu B).
Offline
#7 08. 03. 2014 17:54
- janca361

- .
- Příspěvky: 3284
Re: Tečny k elipse
↑ Sheldon.C:
Není zač.
Příště ještě prosím ještě označ úlohu za vyřešenou (v prvním příspěvku v pravém dolním rohu).
Offline
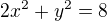 na přímce y=x-2.
na přímce y=x-2.![kopírovat do textarea $A[2,0]$](/mathtex/0e/0ee9c371936c40d19e6e64159245c1bc.gif) a
a ![kopírovat do textarea $B[-\frac{2}{3},\frac{4}{3}]$](/mathtex/50/5033c28739e4ba1cb787cbafa1482158.gif) , ale můj výsledek mi nesouhlasí s výsledkem uvedeným.
, ale můj výsledek mi nesouhlasí s výsledkem uvedeným.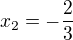 a druhá souřadnice tedy
a druhá souřadnice tedy 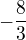 . Ale i tak to pořád nevychází podle výsledku, který má být
. Ale i tak to pořád nevychází podle výsledku, který má být