Matematické Fórum

janca361 · 17. 03. 2014 18:01

Ahoj, mám příklad:
Napište rovnici kružnice, která se dotýká přímky 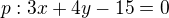$p: 3x+4y-15=0$ , její střed leží na přímce 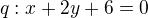$q:x+2y+6=0$ a její poloměr je $r=5$ .

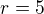Příklad se tu již řešil:Odkaz
Jen nechápu, co jsou zač ty dvě přímky, o kterých píše Marian.

Marian napsal(a):
↑↑ maisie:
Pokud by stačila středová rovnice kružnice, která má tvar
$(x-m)^2+(y-n)^2=r^2,\qquad r>0,$
pak máš vlastně zjistit celkem tři parametry, které se v ní vyskytují. Jsou to

* poloměr r,
* x-ová souřadnice středu kružnice m,
* y-ová souřadnice středu kružnice n.

Je již dáno r=5 zadáním. Stačí tedy zjistit souřadnice středu. Ty ovšem leží na přímce q: x+2y+6=0. Navíc hledaná kružnice se má dotýkat přímky p: 3x+4y-15=0. Pokud si načrtneš situaci, zjistíš, že stačí k přímce p najít dvě přímky s ní rovnoběžné, třeba je označím p1 a p2, jejichž vzdálenost bude od přímky p rovna hodnotě 5. Rovnice musí mít tvar
$p_1:\qquad 3x+4y+c_1=0,\qquad\qquad p_2:\qquad 3x+4y+c_2=0.$
Ta čísla c1 a c2 se musí spočítat. Neměl by to být problém, protože velikost normálového vektoru přímky p je rovna zrovna pětce (odmocnina(3*3+4*4)=odmocnina(25)=5). Střed(y) hledaných kružnic tedy musí ležet kromě na přímce q ještě i na přímce p1 nebo p2. Tz., že stačí spočítat jen průsečíky dvojic přímek (q,p1) a (q,p2). To budou souřadnice středů, tj. $S_1=[m_1,n_1]$ a $S_2=[m_2,n_2]$ .

Já jsem postupovala takto (a skončila ve slepé uličce):
Moje představa:

Autor skryl část textu. Zobrazit/skrýt!

$S[m;n]$
$k: &(x-m)^{2}+(y-n)^{2}=r^{2} \\ &(x-m)^{2}+(y-n)^{2}=25$

$q: &x+2y+6=0 \\ S \in q: &m+2n+6=0$

$T[x_0;y_0]$
$p=t:&3x+4y-15=0 \\ &t:(x-m)(x_0-m)+(y-n)(y_0-n)=r^{2}$

Předem díky za rady.

zdenek1 · 17. 03. 2014 18:50

↑ janca361:
Marianovy přímky jsou rovnoběžky s přímkou $p$ ve vzdálenosti 5. Jejich průsečíky s $q$ jsou pak středy.

K tvému postupu:
z rovnice 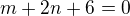$m+2n+6=0$ dostáváš 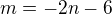$m=-2n-6$ , takže bod $S[-2n-6;n]$
vzdálenost středu od tečny je rovna poloměru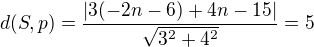
$d(S,p)=\frac{|3(-2n-6)+4n-15|}{\sqrt{3^2+4^2}}=5$
Vyřešíš a je to

janca361 · 17. 03. 2014 18:58

↑ zdenek1:
Hustý. Pravda, že já si nikdy se vzdálenostma moc netykala.

Díky.

Matematické Fórum

#1 17. 03. 2014 18:01

Rovnice kružnice se středem na zadané přímce

Marian napsal(a):

#2 17. 03. 2014 18:50

Re: Rovnice kružnice se středem na zadané přímce

#3 17. 03. 2014 18:58

Re: Rovnice kružnice se středem na zadané přímce

Zápatí