Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 15. 03. 2009 00:52
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: goniometricne rovnice
využitím identity  a definičního vztahu
a definičního vztahu  máme
máme , vynásobíme cos x
, vynásobíme cos x , odečteme sin x
, odečteme sin x , závorku rozložíme jako rozdíl čtverců
, závorku rozložíme jako rozdíl čtverců
Aby mohl být součin nalevo nulový, musí být nulový jeden z činitelů. To nám dává tři jednoduché rovnice, pro které snadno zjistíme řešení.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#4 15. 03. 2009 07:29
- marnes

- Příspěvky: 11227
Re: goniometricne rovnice
↑ StupidMan:Nemělo by se dělit, násobit v rovnici můžeme. Možná si to násobení pleteš s nerovnicemi, tam je to problém. Když chceš násobit u nerovnice, musíš 100% vědět, jestli je to výraz kladný nebo záporný. Když to nevíš, nebo nemůžeš omezit, tak si to dovolit nemůžeš.
Jo. A na začátku vás zdravím.
Offline
#6 15. 03. 2009 13:49
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: goniometricne rovnice
sin x + sin 2x - sin 3x = 0
sin x + 2sin x cos x - sin 2x cos x - sin x cos 2x = 0
sin x + 2sin x cos x - 2 sin x cos^2 x - sin x cos 2x = 0
sin x (1+ 2 cos x - 2 cos^2 x - cos 2x) = 0
sin x (1+ 2 cos x - 2 cos^2 x - (1 -2 cos^2x)) = 0
sin x (2 cos x) = 0
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#7 15. 03. 2009 16:38
Re: goniometricne rovnice
Dík moc ;) Prosim tě, pomohl bys mi ještě se dvouma příkladama na gon. funkce?Mě tohle zrovna moc nejde. Vlastně vůbec.
sin 2y lomeno 1 + cos 2y + 1- cos 2y lomeno sin 2y =
Nvm, jak mám napsat lomeno, ale tak snad ej to aspon trosku pochopitelny:-)
a druhej přiklad:
2 cos x ( cos je na druhou) = ( odmocnina ze 3 - 4 (jenom 3 je pod odmocninou) ) * cos x + 2 odmocnina ze 3
Taky je to jaks taks doufam srozumitelny, jak jsem to napsal:-) dík za pomoc
Offline
#9 15. 03. 2009 16:52
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: goniometricne rovnice
↑ KarlikIV:
1) Rozlož podle vzorců pro sin2x a cos2x (2sinxcosx; cos^2 x - sin^2 x)
↑ KarlikIV: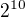 = 2^{10}
= 2^{10} = cos^2 x
= cos^2 x
Offline
#11 15. 03. 2009 17:11
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: goniometricne rovnice
↑ KarlikIV:
A co na tom neumíš? Prostě místo 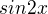 napíšeš
napíšeš  .
.
Offline
#13 15. 03. 2009 23:47
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: goniometricne rovnice
↑ KarlikIV:
Zdravím :-)
ne, že by mi chtělo luštit, co je v zadání, ale snad jsem to rozluštila a začala bych takto: 
Zde bych použila úpravu, kterou doporučuje kolega halogan.
Také doporučuji vzit si tabulky nebo něco online na "goniometrické vzorce" a nastudovat si to pořádně, jinak to nebude mít úspěch.
A pozor na definiční obory.
------------------------
Pro kolegy Kondra a marnesa
- moc vás prosím, neřikejte, že je možné dělit nebo násobit výrazem s neznamou jen tak (v rovnicich také) - opravdu se zapomíná ihned doplnit, jaké je omezení v definičním oboru.
Já vím, že vý to víte a nezapomínate :-)
Vzníkají z toho jen ztracené body na přijimačnách a na dalších písemkách.
Zapomínají, a zapomínají, a zapomínaji - nedá se níc dělat, než natvrdo zakázat jak dělit, tak i násobit. Ať to kolegové, co to teprve cvičí, řádně rozepisují ze součínových a podílových tvarů.
Děkuji vám za pochopení.
Offline
#15 16. 03. 2009 00:28
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: goniometricne rovnice
↑ halogan:
Zdravím :-)
Tvůj návrh se těžce TeXoval - nešlo použit copy-paste.
Ručně bych také nevypisovala tolik kroku - ale kolega vypadá dosti bezradně, tak jsem rozepsala.
Df se vztahovalo k uplně prvním příspěvkům v tématu.
Offline
#17 16. 03. 2009 18:38
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: goniometricne rovnice
↑ halogan:
Zdravím :-)
včera jsem měla trochu jiné plány a záměry, než se za 2 minuty dostat ke dvou tg - tak jsi to myslel?
Ale bez korigování Df - to asi nechytám:
podmínky: cos(y) nesmí být 0, sin(y) nesmí být 0
Nebo ne?
--------------------------------------
2. Zadání od KarlikIV (toť otázka, jak to kolega myslel - zda to je ono?)
Offline
#18 22. 03. 2009 17:10
Re: goniometricne rovnice
ahojky prosim nepmohl by mi někdo s těmito úlohami?
1.) Vypočítejte velikost vnitřních úhlů v trojuhelniku ABC jehož delky jsou : a= 6,9 cm b= 4,3cm c= 3,1cm
2.)V trojúhelníku ABC je : a=51,34 b= 34,75 a gama =64°30´ . Vypočítejte c,alfu,betu.
děkuji moc
Offline
#19 22. 03. 2009 17:14
Re: goniometricne rovnice
Ahoj
1) Kosinova věta
2) To samé. Přímo vypočteš stranu c a pak třeba i podle Sinova věta spočteš zbylé úhly
oo^0 = 1
Offline
.png) R na intervalu <0,pi>
R na intervalu <0,pi>

