Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Komplexní integrál pomocí reziduí (TOTO TÉMA JE VYŘEŠENÉ)
#1 12. 04. 2014 16:06 — Editoval jirakst (12. 04. 2014 16:19)
Komplexní integrál pomocí reziduí
Ahoj,
už několik dní se trápím s jedním příkladem, který se mi vypočitat. Některé dílčí postupy, které se mi podařilo různě vyzjistit většinou nechápu zcela a tak velmi uvítám i případný komentář. Díky.
Příklad je následující:
Vypočtete pomocí reziduí integrál 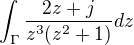 , kde Γ:|z−1−j|=2 je kladně orientovaná kružníce.
, kde Γ:|z−1−j|=2 je kladně orientovaná kružníce.
Offline
- (téma jako vyřešené označil(a) jirakst)
#2 12. 04. 2014 21:09 — Editoval jelena (12. 04. 2014 21:10)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Komplexní integrál pomocí reziduí
Zdravím,
zkusme pomocí vašeho materiálu projít dílčí postupy. Póly jsi určil? Kružnici zakreslil? Jak jsou póly umístěny - našel? Rezidua vypočítal? Děkuji.
Edit: duplicitní téma jsem před časem zamkla a označila za vyřešené - "odznačovat" - to mu nepomůže.
Offline
#3 12. 04. 2014 21:17 — Editoval grizzlybear (12. 04. 2014 21:32)
- grizzlybear

- Příspěvky: 27
- Škola: MFF UK
- Pozice: student
- Reputace: 1
Re: Komplexní integrál pomocí reziduí
nevím, jestli moje rada bude užitečná.
Záčátek úvah:
Já se dostal k nakreslení kružinice se středem v 1, j a poloměrem 2 v komplexní rovině. Dál jsem řešil, kde jmenovatel havaruje. To je v nule "třikrát". A v +- j.
Přičemž +j je v kružnici a -j tam není, tudíž tuším nemá vliv na integrál. A pak je tam myslím vzorec na výpočet reziduí a ten si nepamatuju. :)
Krok 2
na wiki jsem našel:
http://en.wikipedia.org/wiki/Residue_%2 … nalysis%29
Limit formula for higher order poles
- tenhle vzorec jsem použil na 0 a tu považuju za pól 3. řádu.
jestli jsem správně poderivoval a limitil, vyšlo mi:
Res(f(z), 0)=-2*j
Offline
#4 12. 04. 2014 23:01
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Komplexní integrál pomocí reziduí
↑ grizzlybear:
Zdravím a děkuji za ochotu, ovšem jde o zadání samostatné práce (dohled - to je můj speciální koníček :-) Vzorce a postupy jsou podrobně ve studijním materiálu kolegy ↑ v odkazu:, úlohy se objevuji každý rok, tak by se něco našlo i s předchozích let. Tedy kolega může prokázat více samostatné snahy viz pravidla (a navíc se to nepohodlně vypisuje).
Správnost jsem zatím nekontrolovala, to může kolega.
Offline
#5 13. 04. 2014 13:50
- grizzlybear

- Příspěvky: 27
- Škola: MFF UK
- Pozice: student
- Reputace: 1
Re: Komplexní integrál pomocí reziduí
↑ jelena:
nevím, jestli jsem tu zprávu úplně pochopil, ale zkrátka mu nemám přímo ten příklad počítat (byť možná špatně). Pravidla fóra jsem zatím moc neřešil, pardón. :)
Offline
#6 13. 04. 2014 15:47 — Editoval jelena (13. 04. 2014 18:13)
Re: Komplexní integrál pomocí reziduí
Ahoj,
děkuji za pomoc s reziui a znovuotevření vlákna. Přes 2 hodiny jsem studoval sbírku a příklad bych zatím zapsal nějak takto:
Jelena: úprava TeX: (3.stupeň),
(3.stupeň), 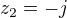 (1.st),
(1.st),  (1.st)
(1.st)
Dále jsem si nakresil kružnici
![kopírovat do textarea $S=[1,+j], r=2$](/mathtex/d9/d976c79b33a6666e2477c35e12833b02.gif) - toho vyplynulo, že z Cauchy-Riemanovych podmínek(nepočital jsem, ale asi budou platit) je funkce holomorfní pro
- toho vyplynulo, že z Cauchy-Riemanovych podmínek(nepočital jsem, ale asi budou platit) je funkce holomorfní pro  , což vyšlo grizzlybearovi (děkuji).
, což vyšlo grizzlybearovi (děkuji). Pro pól prvního řádu mi pak vyšlo
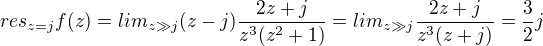 a pro ten 3. řádu
a pro ten 3. řádu ![kopírovat do textarea $res_{z=0}f(z)=\frac{1}{2!}lim_{z\gg j}\frac{d^{2}}{dz^{2}}[\frac{2z+j}{(z^{2}+1)}]$](/mathtex/8c/8cfac0e57c0cdf981329930ffa4673b1.gif)
Tady jsem se zaseknul, protože asi neumím parciální derivace, resp. mi vyšlo, že neplatějí Cauchyho podmínky a když jsem derivoval funkci vyšlo
 , což se mi taky moc nezdá, tak nevím. Nejvíce se teď řeším, jak se vlastně derivuje to j.
, což se mi taky moc nezdá, tak nevím. Nejvíce se teď řeším, jak se vlastně derivuje to j. Offline
#7 13. 04. 2014 18:24
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Komplexní integrál pomocí reziduí
↑ grizzlybear:
:-) pravidla jsi řešil při registraci (jsou striktně pro dotaz, ale jen doporučení pro odpověď). Tk přiměřeně (samozřejmě, nemůžeš vědět, že je to samostatná práce).
↑ jirakst:
trochu jsem přepsala úvod - nebyl čitelný. A děkuji za samostatnou snahu. Kružnice a póly mám také stejně, první res také. Pro derivace: j je konstanta, derivuje se po proměnné z. Tedy 1. derivace opravit jen hned na začátek  .
.
Pokud jsem nic nepřehlédla (jinak derivace můžeš překontrolovat i v WA).
Offline
#8 13. 04. 2014 19:00 — Editoval jirakst (13. 04. 2014 19:06)
Re: Komplexní integrál pomocí reziduí
↑ jelena:
Děkuji za kontrolu.
O Wolfram jsem se pokoušel, jen jsem se k němu nemohl přes brzké odpoledne nějak doklikat (přetížený server?) :D
Nějak mi vyšlo i to druhé reziduum (3. stupně) a to ![kopírovat do textarea $resf(z)_{z=0}=\frac{1}{(3-1)!}lim_{z\gg 0}\frac{d^{3-1}}{dz^{3-1}}[(z-0)^{3}\frac{2z+j}{z^{3}(z^{2}+1)}]=\frac{1}{2}lim_{z\gg 0}\frac{2(2z^{3}+3jz^{2}-6z-j}{(z^{2}+1)^{3})}=-j$](/mathtex/a2/a2bb5014933f08c0b2315c71946ae29c.gif)
Je to velice podobné tomu, co vyšlo grizzlybearovi, jen tam asi vypadl ten faktoriál ze vzorce (teda pokud je toto správně).
Offline
#9 13. 04. 2014 19:11
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Komplexní integrál pomocí reziduí
↑ jirakst:
já jsem zadala do WA a shoduje se to (-j nebereme, jak se dohodlo).
Offline
#10 13. 04. 2014 20:31
Re: Komplexní integrál pomocí reziduí
OK. Mockrát děkuji, že jste mi pomohli, měl jsem poslední možnost získat body na zápočet a donutilo mě to pochopit i přechozí látku :D
Můžu mít ještě jednu otázku? Projeví se nějak v tomto příkladu, kdyby křivka  nebyla provotočivá nebo je to v zadání jen pro zmatení nepřítele (studenta)?
nebyla provotočivá nebo je to v zadání jen pro zmatení nepřítele (studenta)?
Offline
#11 14. 04. 2014 00:10
- grizzlybear

- Příspěvky: 27
- Škola: MFF UK
- Pozice: student
- Reputace: 1
Re: Komplexní integrál pomocí reziduí
↑ jirakst:
Podle mě to tam není kvůli zmatení. V tom tvým textu je Reziduová věta a tam se mluví o kladné orientaci křivky. A kladná je proti směru hodinových ručiček... a to reziduum jsem patrně zapomněl vydělit 2.
Offline
#12 14. 04. 2014 00:36
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Komplexní integrál pomocí reziduí
↑ jirakst:
také děkuji (a kolegovi ↑ grizzlybear:). Také bych to tak viděla, jako kolega ohledně orientace křivky (pro opačnou orientaci by se ještě použila věta z úvodů kapitoly 5.1 Integrál komplexní proměnné (nad příkladem 5.1.1)).
Offline
#13 14. 04. 2014 11:11
Re: Komplexní integrál pomocí reziduí
Aha, teď už tomu rozumím podstatně více (jde o, že by se přehodily integrační meze(?)).
Můžu ještě prosím požádát o konečnou kontrolu výsledku (do wolframu se mi to nepodařilo dát)?
Děkuji.
Offline
#14 14. 04. 2014 14:04
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Komplexní integrál pomocí reziduí
↑ jirakst:
změna směru orientace zde by měla vliv jen na znaménko výsledku. Jinak Výsledek Tvého integrálu mi vyšel stejně.
Offline
#16 14. 04. 2014 21:33
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Komplexní integrál pomocí reziduí
↑ jirakst:
děkuji i za příspěvek.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Komplexní integrál pomocí reziduí (TOTO TÉMA JE VYŘEŠENÉ)
