Matematické Fórum

O.o · 15. 03. 2009 16:05 — Editoval O.o (15. 03. 2009 16:21)

Ahoj .-),

po delší době se ozývám a ne zrovna v mnou často navštěvované sekci, zasekl jsem se u jedné úlohy z fyziky a nevím jak nato, mohl bych vás požádat o pomoc, prosím? Fyzika se semnou zatím odmítá přátelit -).

Jde o jednoduchý příklad (počátek kapitoly) na rychlost hmotného bodu.

Příklad 2/4

Našel jsem si k tomu ve skriptech tabulku:

Tabulka

Usoudil jsem, že půjde asi o přímočarý pohyb zrychlený, tak uvažuji nad použitím vzorce: $x=\frac{1}{2}at^2+v_0t+x_0$ , ale přes to jsem se k výsledku ani jednou nedostal. Musím říct, že vůbec nevím, jak na tenhle příklad a to už jsem si říkal, že tuhle část relativně zvládám.

Děkuji za případnou pomoc ;-).

Postupoval jsem:

x(t) - pohybová funkce (závislost na t jako na čase), x_0 nějaká počáteční hodnota, funkci x(t) jsem bral jako funkci pro dráhu (došlo k přetypování s(t) = x(t) a s_0 = x_0).

Na počátku dráha nulová, tedy s_0 mizí, dále jsem derivoval pro získání závislosti rychlosti na čase.

$s(t)=\frac{1}{2}at^2+v_0t+s_0 \ \rightarrow \ v(t) = at+v_0$

To ale k cíli nevede a nějak mi to ani nehraje, něco jsem špatně pochopil a pak dal asi dohromady další něco, což spolu nefunguje, původně jsem to dělal jinak, ale také nefugunje .-)

jelena · 15. 03. 2009 17:46 — Editoval jelena (15. 03. 2009 17:46)

↑ O.o:

Zdravím :-)

jen jedna drobnost - zrychlení se mění - to znamená, že nemůžeš používat vzorec z tabulky pro pohyb rovnoměrně zrychlený, ale musíš využit své znalosti funkcí a to tak, že začneš od zrychlení a = f(t) lineární funkce.

Zrychlení je 2. derivace drahy po t a máš se dostat zpět k draze - tedy integruj.

OK?

Čas sice nemám, ale když jsem dostala takový šok (pozitivní), jak jsi v tématech fyziky, že jsem reagovala.

jelena · 15. 03. 2009 17:50

↑ jelena:

V úloze chtěji rychlost, přehledla jsem - rychlost je 1. derivace dráhy,
zrychlení je 1. derivace rychlosti a 2. derivace drahy.

O.o · 15. 03. 2009 19:05

↑ jelena:

Zdravím po delší době :-),

snad jsem nezpůsobil moc velký šok a zkusím příště varovat předem =o).

Teorii co jsi psala, tak nějak ještě chápu, dokoncei nějaká ta grafická zdůvodnění, co nám k tomu ukazovali na přednáškách (i to by ještě šlo), ale jsem neschopný to správně aplikovat. Můj původní výpočet (to jsem ještě neotevřel skripta ;)) byl řešený jako funkce, kde jsme derivoval/integroval, ale už nevím co ani jak, vkaždém příapdě nic nevyšlo .-).

Když vezmu tedy dráhu jako nějakou funkci x závislou na t, tedy x(t), pak $x''(t) = 5 \ m \cdot s^{-2} = a \ \rightarrow \ x'(t) = 5t+x_{0} \ m \cdot s^{-1} = v \ \rightarrow \ x(t) = \frac{5}{2}t^2+x_0t+x_{0}^{#}$ , kde x_0 je počáteční rychlost, x_{0}^{#} je souřadnice v t=0s.

Teď to přepíši, aby v těch x nebyl takový nepořádek: $x(t) = \frac{5}{2}t^2+v_0t$ - s tím, že x_{0}^{#} je 0m, dosadím počáteční rychlost, aby tma nebylo tolik konstant a mám: $x(t) = \frac{5}{2}t^2+10t \ [m]$ , což se jaasně nerovná výsledku za c). Nebýt pětky v čitateli, tak se to podobá výsledku za b) (začínám si znovu připadat trochu komicky) =oD.

Někde dávám dohromady něco neslučitelného nebo používám něco nepoužitelného, prosím vyslechne někdo volání o pomoc zoufalého námořníka, který se potápí v neznámých vodách? ;-)

O.o · 15. 03. 2009 20:22 — Editoval O.o (15. 03. 2009 20:22)

Tak jsem změnil výpočet.

Vezmu to tak, že a stoupá rovnoměrně s časem, takže grafem bude přímka.

Pak tedy tuto přímku mohu zapsat ve tvaru y=kx+q, posunutí po ose y žádné není (čas nula <=> zrychlení nula), tedy píši y=kx, k je směrnice (vrátím se k ní během okamžiku) a x přepíši jako čas (t; abych dostal závislost na čase), tedy píši, že y=kt. Nakone ještě pro jasnost přeznačím y=a, tedy píši přímku jako a=kt.

Vím, že v čase t=10s je a=5, tedy: $a=kt \ \rightarrow \ 5=k10 \ \Rightarrow \ k=\frac{1}{2}$ píši tedy přímku ve tvaru: $a=\frac{1}{2}t$ .

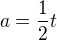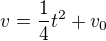Dále pokračuji ze vztahu okamžitého zrychlení v závislsoti na čase: $a=\frac{dv}{dt}$ , neřeším teď vektory jsem jen v jedné ose. $a=\frac{dv}{dt} \ \Rightarrow \ adt=dv \ \rightarrow \ \int{adt}=v \ \rightarrow \ \int{\frac{1}{2}tdt}=v \ \Rightarrow \ v=\frac{1}{4}t^2+C_1$ , z počátečních podmínek bude C_1=v_0, kde v_0 je počáteční rychlost, tedy: $v=\frac{1}{4}t^2+v_0$ - to je odpověď pro zadání b), respk.: $v=\frac{1}{4}t^2+10$

Pokračuji podle vztahu: $v=\frac{ds}{dt} \ \Rightarrow \ vdt=ds \ \rightarrow \ \int{vdt}=s \ \rightarrow \ \int{(\frac{1}{4}t^2+v_0)dt}=s \ \rightarrow \ s=\frac{1}{12}t^3+v_0t+C_2$ , z počátečních podmínek konstantu zavedu jako C_2=s_0, kde s_0 je počáteční souřadnice (tedy nula) a píši, že s jako dráha je: $s=\frac{1}{12}t^3+10t$ a to je odpověď pro zadání za c).

Může to takhle prosím být?

jelena · 15. 03. 2009 20:36

↑ O.o:

no samozřejmě, jak jinak:-)

---------
Je zle, když dojde proviant, je zle, když přijdou kurděje, Ale běda, třikrát běda těm, co chybí naděje!

O.o · 15. 03. 2009 23:04

↑ jelena:

Děkuji moc, já se zase určitě zítra ozvu s jiným pohybem nebo něčím podobným ;-).

PS: Kam na ty songy chodíš? .-)

jelena · 15. 03. 2009 23:56

↑ O.o:

To se určitě ozví - totiž proto vás (nás) v 1. pololetí cvičí analýzu, abyste pak všechno zvladli. A je ušetřeno spoustu námahy - zejména, když vím, že analýzu zvládaš velice slušně.

Jelikož pák budou chemické procesy kontinuální, co plynou v časě a třeba tady kolega lukashz byl docela unešen vaši knihou:

http://forum.matweb.cz/viewtopic.php?id=6644

--------
PS: dřívě na koncerty, ale teď jsme konstatovali, že všeho je nějak malo (Traband třeba změnil styl, tak si moc "neladíme" a teď vůbec nehraji - ale, nevadí - hlavně ať jsou v pořádku) tak teď chodím do vlastní hlavy.

Zdravím :-)

Matematické Fórum

#1 15. 03. 2009 16:05 — Editoval O.o (15. 03. 2009 16:21)

Pohyb hmotného bodu

#2 15. 03. 2009 17:46 — Editoval jelena (15. 03. 2009 17:46)

Re: Pohyb hmotného bodu

#3 15. 03. 2009 17:50

Re: Pohyb hmotného bodu

#4 15. 03. 2009 19:05

Re: Pohyb hmotného bodu

#5 15. 03. 2009 20:22 — Editoval O.o (15. 03. 2009 20:22)

Re: Pohyb hmotného bodu

#6 15. 03. 2009 20:36

Re: Pohyb hmotného bodu

#7 15. 03. 2009 23:04

Re: Pohyb hmotného bodu

#8 15. 03. 2009 23:56

Re: Pohyb hmotného bodu

Zápatí