Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Teorie grup - podgrupy (TOTO TÉMA JE VYŘEŠENÉ)
#1 12. 05. 2014 20:58 — Editoval Akcope (12. 05. 2014 21:08)
Teorie grup - podgrupy
Zdravím, prosil bych o vysvětlení jak hledat podgrupy v nějaké konkrétní zadané grupě.
Definici podgrupy znám, také vím že každá grupa má jako podgrupy jednotkový prvek a sebe samu.
Nicméně vůbec netším jak najít všechny ostatní podgrupy. Jak postupovat nějak systematicky, aby člověk na žádnou nezapomněl? Je na to nějaká metoda?
Typický příklad na toto by bylo : Najděte všechny podgrupy v grupě 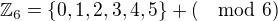
Předem děkuji za odpověď.
Offline
- (téma jako vyřešené označil(a) Akcope)
#2 12. 05. 2014 21:54 — Editoval vanok (12. 05. 2014 21:55)
Re: Teorie grup - podgrupy
Ahoj ↑ Akcope:,
Akoze tvoja groupa je radu 6, vieme ze vsetki jej podgrupy budu mat rad co bude delitel 6.
Pre rad 1, podgrupa je 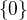 ( sme v aditivnom oznaceny, tak je to grupa formovana nulovym prvkom.
( sme v aditivnom oznaceny, tak je to grupa formovana nulovym prvkom.
Pre rad 2, podgrupa je 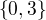
Pokracuj.
V tomto pripade je to ozaj jednoduche, ale vseobecne to moze byt komplikovanejsie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Teorie grup - podgrupy (TOTO TÉMA JE VYŘEŠENÉ)
