Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Stredná hodnota - ruleta (TOTO TÉMA JE VYŘEŠENÉ)
#2 21. 05. 2014 20:14
Re: Stredná hodnota - ruleta
↑ tomson:
Zdravím,
jako nejschůdnější se mi jeví následující postup: jako 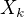 označíme náhodnou proměnnou, která popisuje počet různých čísel při
označíme náhodnou proměnnou, která popisuje počet různých čísel při  kolech rulety. Najdeme rekurenční vztah mezi
kolech rulety. Najdeme rekurenční vztah mezi ![kopírovat do textarea $\mathbb{E}[X_k]$](/mathtex/c3/c366ee57089036421c202e1b8eddddc7.gif) a
a ![kopírovat do textarea $\mathbb{E}[X_{k-1}]$](/mathtex/cf/cfb7dd11137c5def7f7cf59d5e1b3e36.gif) a na základě toho vyjádříme
a na základě toho vyjádříme ![kopírovat do textarea $\mathbb{E}[X_{k}]$](/mathtex/b0/b09662be6ddeb782cc92ca9a0c0b6b40.gif) jako funkci
jako funkci  . A tím i získáme odpověď na otázku, jaká je hodnota
. A tím i získáme odpověď na otázku, jaká je hodnota ![kopírovat do textarea $\mathbb{E}[X_{37}]$](/mathtex/11/11251b829b3261c4b4d4fe67a96e652a.gif) .
.
Offline
#3 21. 05. 2014 22:12
Re: Stredná hodnota - ruleta
↑ vnpg:
Takže šlo by to tým spôsobom, že ak si označím  pravdepodobnosť, že mi v ďalšom kole padne iné číslo ako v predchádzajúcich, tak potom platí:
pravdepodobnosť, že mi v ďalšom kole padne iné číslo ako v predchádzajúcich, tak potom platí: ![kopírovat do textarea $\mathbb{E}[X_k]=p(\mathbb{E}[X_{k-1}]+1)+(1-p)\mathbb{E}[X_{k-1}]$](/mathtex/83/83b53556077e218dceab5938aea06644.gif) , teda
, teda ![kopírovat do textarea $\mathbb{E}[X_k]=\mathbb{E}[X_{k-1}]+p$](/mathtex/12/12fc625d12a09ad087f292d522c2f35a.gif)
Ak áno, tak by som ešte potreboval pomôcť s vyjadrením tej pravdepodobnosti 
Offline
#4 21. 05. 2014 23:30
Re: Stredná hodnota - ruleta
↑ tomson:
Takto bychom mohli postupovat v případě, že by pravděpodobnost  nezávisela na počtu různých čísel, která padla v prvních
nezávisela na počtu různých čísel, která padla v prvních  kolech. Tak tomu ale bohužel v našem případě není - pokud v prvních
kolech. Tak tomu ale bohužel v našem případě není - pokud v prvních 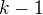 kolech padlo řekněme
kolech padlo řekněme  různých čísel, potom máme pravděpodobnost
různých čísel, potom máme pravděpodobnost 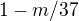 , že v
, že v  -tém kole padne číslo, které do té doby nepadlo. Takže potřebujeme trochu jiný postup.
-tém kole padne číslo, které do té doby nepadlo. Takže potřebujeme trochu jiný postup.
Můžeme vyjít z následujícího vztahu, který platí pro všechna celá čísla 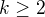 a
a 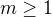 :
:
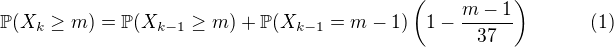 .
.
Jeho platnost lze zdůvodnit celkem snadno: jev, kdy v prvních  kolech padne alespoň
kolech padne alespoň  různých čísel, nastane v jednom z následujících dvou vzájemně neslučitelných případů: (a) alespoň
různých čísel, nastane v jednom z následujících dvou vzájemně neslučitelných případů: (a) alespoň  různých čísel padlo již v prvních
různých čísel padlo již v prvních  kolech; (b) v prvních
kolech; (b) v prvních  kolech padlo přesně
kolech padlo přesně 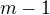 různých čísel a v
různých čísel a v  -tém kole padne některé z těch ostatních.
-tém kole padne některé z těch ostatních.
Dále použijeme následující výsledek: Je-li  náhodná proměnná s hodnotami v
náhodná proměnná s hodnotami v 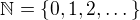 , pak lze střední hodnotu
, pak lze střední hodnotu  vyjádřit následujícími dvěma způsoby:
vyjádřit následujícími dvěma způsoby:
![kopírovat do textarea $\mathbb{E}[Y] = \sum_{m = 1}^\infty m \mathbb{P} (Y = m)$](/mathtex/59/59ec5e92fdb76614d8670b5a56681d08.gif) a
a ![kopírovat do textarea $\mathbb{E}[Y] = \sum_{m = 1}^\infty \mathbb{P} (Y \geq m)$](/mathtex/03/03a658528e4d7feb6abb3eb2853d4014.gif) .
.
A nyní již máme asi to nejtěžší za sebou: s pomocí obou uvedených výrazů pro střední hodnotu a vztahu 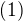 odvodíme rekurenční vztah mezi
odvodíme rekurenční vztah mezi ![kopírovat do textarea $\mathbb{E}[X_k]$](/mathtex/c3/c366ee57089036421c202e1b8eddddc7.gif) a
a ![kopírovat do textarea $\mathbb{E}[X_{k-1}]$](/mathtex/cf/cfb7dd11137c5def7f7cf59d5e1b3e36.gif) a další kroky jsou již otázkou poměrně snadných hrátek se symboly.
a další kroky jsou již otázkou poměrně snadných hrátek se symboly.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Stredná hodnota - ruleta (TOTO TÉMA JE VYŘEŠENÉ)

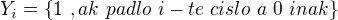
![kopírovat do textarea $\mathbb{E}[X]=\sum_{i=1}^{37}\mathbb{E}[Y_{i}]$](/mathtex/fc/fcbdc58c0b65d0b14c73a8039cf19e87.gif)
![kopírovat do textarea $\mathbb{E}[Y_{i}]=\mathbb{P}(Y_{i}=1)=1-\mathbb{P}(Y_{i}=0)=1-({36}/{37})^{37}$](/mathtex/50/5022bd20ed90e27437cacdd7c644a660.gif)
![kopírovat do textarea $\mathbb{E}[X]=37(1-(36/37)^{37})\doteq23.57$](/mathtex/40/40b4d1e469353cbbb0da3a2d0d88dab2.gif)
![kopírovat do textarea $\mathbb{E}[X_k] = 1 + \frac{36}{37} \mathbb{E}[X_{k-1}]$](/mathtex/dd/dd5b2fe5e44b851a53d252602a0ceb5a.gif) a odtud
a odtud ![kopírovat do textarea $\mathbb{E}[X_k] = 37 (1 - (36/37)^k)$](/mathtex/b6/b62ee5f7b23c052483ae7793450c8081.gif) .
.