Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 12. 06. 2014 22:00 — Editoval Spalker (12. 06. 2014 22:15)
Nerovnice
Dobrý den, měl bych dotaz co se týče určování množiny čísel.. Vím, že se v jednom topicu nemají řešit 2 příklady, ale v tomto případě to spolu souvisí...
1. PŘÍKLAD: Zadání - Množina všech reálných čísel, pro která platí  je rovna množině?
je rovna množině?
Pro: x>0
Interval: (0,2)
Pro: x<0
Interval: (-2,0)
No a teďka bych se rád zeptal, jestli se mezi těmíto intervaly dělá průnik nebo sjednocení.. ?
V případě, že se dělá sjednocení by to mělo být: (-2,0) u (0,2)
V případě, že by se dělal průnik tak by to měla být prázdná množina..
V tomto příkladě je ve výsledcích správná možnost sjednocení.
2. PŘÍKLAD: Zadání - Množina všech reálných čísel, pro která platí  je rovna množině?
je rovna množině?
Řeším pro jedničku a pro dvojku.
Pro jedničku:
Interval: (-nekonečno, -5) u (5, +nekonečno)
Pro dvojku:
Interval: (-25,25)
No a teďka bych se rád zeptal úplně stejně jako u příkladu č. 1. Dělá se průnik nebo sjednocení?
V případě sjednocení by to mělo být: (-nekonečno,-25) u (25,+nekonečno)
V případě průniku by to mělo být: (-25,-5) u (5,25)
V tomto příkladě je ve výsledcích správná možnost průnik..
Má otázka tedy zní.. Příklady jsou si naprosto totožné.. Co tedy určuje, resp. jak poznám, že jednou budu dělat průnik a po druhé najednou sjednocení? Už jsem se na to ptal v tomto topicu(http://forum.matweb.cz/viewtopic.php?id=75525), ale byl jsem z toho natolik zmatenej, že jsem tam napsal úplně něco jinýho než jsem chtěl..
I když vlastně tam je to ale zadaný tak šikovně, že ať už budeme určovat průnik nebo sjednocení, tak to vyjde stejně pokud se nemýlím..Pro ten příklad na který už jsem se ptal v tom topicu..  .
.
Jinak všechny určování intervalů řeším graficky..
Děkuji za odpověď.
Offline
- (téma jako vyřešené označil(a) Spalker)
#5 12. 06. 2014 22:26 — Editoval gadgetka (12. 06. 2014 22:48)
Re: Nerovnice
K druhému příkladu:
Tento zápis  si můžeš přepsat na dvě nerovnice
si můžeš přepsat na dvě nerovnice
Z první nerovnice získáš dvě množiny, které sloučíš, stejně tak z druhé nerovnice. A ty sloučené množiny z jednotlivých nerovnic v závěru "pronikneš", protože ty nerovnice platí současně. Čili teď mezi těmi množinami udělej průnik. :)
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#6 12. 06. 2014 22:29
Re: Nerovnice
Postupuješ při řešení naprosto správně. Jen je potřeba si uvědomit, kdy se při řešení používá slůvko "nebo" (sjednocení) a kdy "a současně" (průnik). Ta slůvka ti poté pomohou k správnému postupu u výsledného řešení.
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#7 12. 06. 2014 22:37
Re: Nerovnice
No však to jsem udělal ne? Já ty 2 nerovnice myslel právě tím, jak jsem tam napsal, že budu řešit pro jedničku a pro dvojku..
U 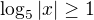 jak jsem již psal mně vyšlo: (-nekonečno, -5) u (5, +nekonečno)
jak jsem již psal mně vyšlo: (-nekonečno, -5) u (5, +nekonečno)
A pro 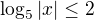 mně vyšlo: Interval: (-25,25)
mně vyšlo: Interval: (-25,25)
Jen tedy nechápu u tvého zápisu proč tam je větší nebo ROVNO .. :/ Pokud ale ten můj postup je správný, tak to možná ani nechci vědět, protože by mě to zmátlo, protože to předpokládám řešíš jiným postupem..
Podle čeho tedy poznám, že mám dělat průnik a kdy sjednocení? Já právěže dělal všude sjednocení a vycházelo mi to dokud jsem nenarazil na takovýhle typy příkladů.. Jenže v nich nevidím rozdíl a nevim podle čeho poznat, že zrovna teďka najednou budu dělat průnik místo sjednocení.. :/
Offline
#8 12. 06. 2014 22:46 — Editoval gadgetka (12. 06. 2014 22:47)
Re: Nerovnice
To byl omyl. :) Jdu to opravit.
Psala jsem automaticky \ge a \le.
A ano, dělal jsi to správně. Já jsem ti tím jen chtěla napovědět, že mezi těmi rovnicemi platí "a současně", proto, že se dílčí řešení v závěru slučuje.
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#9 12. 06. 2014 22:51
Re: Nerovnice
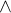 v logice znamená
v logice znamená  v množinách
v množinách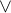 v logice znamená
v logice znamená  v množinách
v množinách
Tam, kde si řekneš "a současně", se dělá průnik. Tam, kde platí "nebo", se dělá sjednocení.
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#10 12. 06. 2014 22:52 — Editoval Spalker (12. 06. 2014 22:53)
Re: Nerovnice
Takže jestli to chápu dobře tedy... V případě, že budu řešit jenom jednu nerovnici jako je například:  , kde vlastně se sice řeší pro x > 0 a pro x < 0 ale furt je to jedna a ta samá nerovnice, tak se bude dělat sjednocení...
, kde vlastně se sice řeší pro x > 0 a pro x < 0 ale furt je to jedna a ta samá nerovnice, tak se bude dělat sjednocení...
A v případě, že budu řešit 2 nerovnice, v tomto případě 1)  2)
2) tak mezi nimi budu dělat průnik, protože to není jedna nerovnice, ale jsou dvě úplně od sebe odlišný... Chápu to dobře? :D
tak mezi nimi budu dělat průnik, protože to není jedna nerovnice, ale jsou dvě úplně od sebe odlišný... Chápu to dobře? :D
Díky moc.. :)
Offline
#11 12. 06. 2014 22:54 — Editoval gadgetka (12. 06. 2014 22:56)
Re: Nerovnice
Mezi definovanou množinou a řešením platí "a současně", proto je tam průnik. Mezi kořeny jednotlivých dílčích kroků platí "nebo", proto se dělá sjednocení.
Mezi např. dvěma nerovnicemi, tak jak máš příklad č. 2, platí "a současně", proto se dělá mezi výslednými kořeny průnik.
Edit: Doplňuji po přečtení tvého dotazu: prakticky ano. Pochopitelně, pokud ty dvě rovnice spolu souvisí, ne, že jedna bude v příkladu 14a) a druhá v příkladu 25b). :D
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline

