Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 02. 07. 2014 09:33 — Editoval MATUTOicek (02. 07. 2014 09:37)
- MATUTOicek
- Příspěvky: 25
- Reputace: 0
Lineární rovnice
Zdravím,
chtěl bych se zeptat na jeden příklad, moc si sním nevím rady, mám lineární rovnici o třech neznámých se čtyrmi řádky, chci jí vypočítat pomocí matice, takže udělám matici a v průběhu počítání bych měl dojít k tomu, že dojde k vynulování jednoho řádku, mě se ovšem podařilo vynulovat pouze levou stranu a na pravé (za = mi zůstalo číslo) jak mám postupovat v takovém případě? Napadlo mě ten řádek prostě nechat ležet jako poslední, ovšem rovnice mi potom nevychází.
** posílám fotku příkladu: https://www.dropbox.com/s/7n3i4g47q44fn … .35.04.jpg i postupu
Děkuji
Offline
#2 02. 07. 2014 10:05
Re: Lineární rovnice
↑ MATUTOicek:
Dobrý den. Pokud Vám takový výsledek vyšel regulérním postupem, pak je soustava rovnic
rozporná a nemá řešení. Postup řešení si jednoduše ověříte zadáním matice zde (řešení
krok po kroku): Odkaz
Pokud se tedy nemýlím.
Offline
#3 02. 07. 2014 10:23
- MATUTOicek
- Příspěvky: 25
- Reputace: 0
Re: Lineární rovnice
Dobrý den,
pokud jsem tam tedy do matice 4x4 zadal mé hodnoty a v posledním kroku mi vyšla matice 4x4 s jedničkami na diagonále, soustava nemá řešení, protože nedošlo k vynulování žádného řádku a tím pádem vznikla 4 řešení pro rovnici a třech neznámých, chápu to tak dobře? Ještě posílám náhled rovnice https://www.dropbox.com/s/bk1o5pxv4eej9 … .20.29.png
Moc děkuji
Offline
#4 02. 07. 2014 10:26
- MATUTOicek
- Příspěvky: 25
- Reputace: 0
Re: Lineární rovnice
Ještě, pokud mám rovnici o 4 neznámých a 5ti řádcích, dám jí do matice 5x5 a vynuluji 2 řádky, opět se jedná o neřešitelnou matici, protože mám pouze 3 řádky a 4 neznámé, respektive rovnici, je to tak? Zítra mě čeká zkouška, takže se potřebuji dobře připravit, algebra není má silná stránka, moc děkuji za pomoc.
Offline
#5 02. 07. 2014 10:54
Re: Lineární rovnice
↑ MATUTOicek:
Ahoj. Připomeň si Frobeniovu větu (resp. Frobeniovu podmínku) .
Offline
#6 02. 07. 2014 12:09
- MATUTOicek
- Příspěvky: 25
- Reputace: 0
Re: Lineární rovnice
↑ Rumburak:
Ahoj, připomněl jsem si ji a pomohlo to, jen mám ještě jednu otázečku (snad už poslední) pokud dám lineární rovnici do matice a chci jí počítat gausovou eliminační metodou, můžu prohodit libovolně 2 sloupce / 2 řádky? Vím že při počítání determinantu, zjišťování hodnosti to jde, ovšem v tomto případě si nejsem jistý, jestli by nedošlo k rozházení celé rovnice, když prohodím x1 s x3 například.
Offline
#7 02. 07. 2014 12:54 — Editoval Rumburak (03. 07. 2014 09:54)
Re: Lineární rovnice
↑ MATUTOicek:
Změnit pořadí jednotlivých řádků rozšířené matice ![kopírovat do textarea $[A|b]$](/mathtex/33/333970cb9247c69bac63325322f03347.gif) je totéž jako změnit pořadí jednotlivých rovnic soustavy,
je totéž jako změnit pořadí jednotlivých rovnic soustavy,
takže to na množinu jejích řešení nemá vliv.
Změna pořadí sloupců matice  by však znamenala jakési "přeznačení" původních neznámých, asi jako
by však znamenala jakési "přeznačení" původních neznámých, asi jako
kdybychom soustavu  nahradili soustavou
nahradili soustavou  ,
,
což v průběhu výpočtu sotva lze doporučit.
Offline
#8 02. 07. 2014 12:56
- MATUTOicek
- Příspěvky: 25
- Reputace: 0
Re: Lineární rovnice
↑ Rumburak:
To je přesně co jsem si myslel, takže se sloupců ani nedotknu, já jenom že se to nabízelo jako příhodná varianta v jednom z příkladů. Děkuji :)
Offline
#9 02. 07. 2014 18:26
- MATUTOicek
- Příspěvky: 25
- Reputace: 0
Re: Lineární rovnice
Ještě mám jednu otázku, počítám tuto rovnici

respektive toto mi vyšlo po Gausově metodě, nyní mám určit parametry, chtěl jsem se zeptat, jestli je nějak dané jaké 2 z druhé rovnice zvolím? Já osobně bych volil 4x3, abych měl za rovná se pětiny.
Offline
#10 02. 07. 2014 19:06
- misaH
- Příspěvky: 13438
Re: Lineární rovnice
↑ MATUTOicek:
Je jedno, ktoré neznáme sa zvolia za parameter.
Offline
#11 02. 07. 2014 19:09 — Editoval vanok (02. 07. 2014 19:10)
Re: Lineární rovnice
Ahoj ↑ MATUTOicek:,
Ako som porozumel druha rovnica ma 3 nezname
Cize mozes vybrat dve z nich ako parametre.
Napr. x_3=p, x_4=q...urcis x_2 a na koniec dosadis vsetko do prvej rovnice à urcis x_1.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#12 02. 07. 2014 19:23
- MATUTOicek
- Příspěvky: 25
- Reputace: 0
Re: Lineární rovnice
Super, moc děkuji za rady - ještě mám jeden dotaz, snad už poslední :) když počítám matici Gausovou eliminační metodou, například v matici 4x4, (x1 x2 x3 | výsledek) a nedojde k vynulování řádku, spočítám jí tak že na diagonále budu mít jedničky a jinak nuly, pokud dojde k vynulování, tak no pokud počítám například matici o čtyřech proměnných a třech řádcích (x1 x2 x3 x4 | výsledek) stačí mi udělat nuly pod diagonálou a na ní ani nemusí být jedničky, chápu to tak dobře?
https://www.dropbox.com/s/zil4xvjvctbk1 … 191438.jpg
Offline
#13 02. 07. 2014 19:55
Re: Lineární rovnice
↑ MATUTOicek:,
Tvoj obrazok sa u mna neotvara.
Jednotky na diagonale to je prakticke, a specialne sa to tyka riesenia systemov.
Pokracovat potom nad diagonalou ( u stvorcovych matic) az do jednotkovej matice ( ak je to mozne), je vlastne podobny postup ako inverzia matice systemu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#14 02. 07. 2014 19:57
- MATUTOicek
- Příspěvky: 25
- Reputace: 0
Re: Lineární rovnice
↑ vanok:
Vlastně mi šlo o to, pokud matice není čtvercová, to mi potom stačí dělat nuly pod diagonálou a na ní vlastně ani nemusí být jedničky, je to tak?
Offline
#15 02. 07. 2014 20:12
Re: Lineární rovnice
↑ MATUTOicek:
Nemusia, pokial mas najst len hornu trojuholnikovu maticu.
Ale ist k jednotkovej moze byt uzitocne.
Ako vzdy, vsetko zavisi od polozenej otazky.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#16 02. 07. 2014 23:28
- MATUTOicek
- Příspěvky: 25
- Reputace: 0
Re: Lineární rovnice
Pěkný večer, tak mám ještě jednu otázečku, příkladech jsem měl u matice určit jaký generuje (nebo ve kterém se nachází? Moc tomu nerozumím) vektorový prostor, pokud se například jedná o matici 3x3 a nedojde k vynulování řádku, je to R^3, pokud třeba 5x4 a nedojde k vynulování, je to R^5? A ještě otázka, pokud bych to měl určit například z lineární rovnice, nebo v ní určit determinant, použiji pouze neznámé a nepočítám to co je za =, je to tak? Moc děkuji
Offline
#17 02. 07. 2014 23:39
Re: Lineární rovnice
Akoze pracujes v matici riadkoch tvoj espace riadkov matice metodov GEM nic ne meni na priestore ktore vektory riadky geneneruju. ... A na konci postupu pozruseni nulovych a rovnakych riadkov ti da vlastne bazu toho priestoru riadkov ( jej dim sa vola riadkova hodnost matice ... Moze sa povedat hodnost, lebo stlpcova hodnost ma tu istu hodnotu)
Staci?
Nevideli ste taketo dolezite uvahy v skole?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#18 02. 07. 2014 23:44
- MATUTOicek
- Příspěvky: 25
- Reputace: 0
Re: Lineární rovnice
↑ vanok:
Bohužel jsem za semestr z algebry moc nepochytil a vše jsem se učil až před zápočtem a teď před zkouškou, snad nevadí že jsem se zeptal, za odpovědi jsem moc vděčný. V tomhle jsem se chtěl pouze ujistit, protože vím, že to bude ve zkoušce a nerad bych chyboval. Někde jsem viděl něco že prostor matice je R^řádky x ^sloupce, ale jednoduše - hodnost matice je báze prostoru, který generuje. Moc děkuji :)
Offline
#19 03. 07. 2014 09:45 — Editoval Rumburak (03. 07. 2014 09:57)
Re: Lineární rovnice
hodnost matice je báze prostoru, který generuje.
Tak za to bys mohl i vyletět. :-) Pokusím se uvést ty pojmy na pravou míru:
K matici  je přířazen její
je přířazen její
- řádkový modul 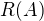 , což je vektorový prostor generovaný jejími řádky,
, což je vektorový prostor generovaný jejími řádky,
- sloupcový modul  , což je vektorový prostor generovaný jejími sloupci.
, což je vektorový prostor generovaný jejími sloupci.
Platí věta, která říká, že oba tyto moduly mají stejnou dimensi - toto číslo se nazývá hodnost matice  .
.
Offline
#20 03. 07. 2014 09:53 — Editoval vanok (03. 07. 2014 09:56)
Re: Lineární rovnice
Zabudol si slovo dimenzia, ako som to pisal
↑ vanok: tu.
Édit : vidim ze ↑ Rumburak: ( pozdravujem) si to podrobne upresnil.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
