Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Báza, modul, priestor ohraničených postupností
#1 24. 08. 2014 19:19 — Editoval kafe_arabica (24. 08. 2014 19:26)
- kafe_arabica
- Příspěvky: 38
- Reputace: 3
Báza, modul, priestor ohraničených postupností
Ahoj.
Potrebujem poradiť, kde v nasledovnej úvahe je chyba.
Priestor ohraničených postupností nad reálnymi číslami je vektorový priestor, teda aj modul, za sčitovanie berieme pozložkové sčitovanie a násobenie skalárom ako pri štandardných konečnorozmerných vekt. pr. Za bázu tohto priestoru môžeme vziať postupnosti typu (1,0,0,....); (0,1,0,0,...) etc. Teda ide o voľný modul.
Vždy hovorím o ľavých moduloch.
Definícia, modul E nad okruhom A nazveme voľným, ak existuje izomorfizmus  , kde
, kde  , pričom
, pričom  .
.
Tzn., že existuje izomorfizmus  , kde Post je priestor ohraničených postupností.
, kde Post je priestor ohraničených postupností.
A tu nastáva moment, kedy neviem, čo je správne. V priestore Post mám postupnosť, ktorá nemá konečný nosič, ale v priestore R^(N) sú postupnosti len s konečným nosičom, a predsa sú tieto priestory izomorfné.
Je chyba v tom, že z tej bázy sa nedá vygenerovať celý priestor Post? Lebo mám taký pocit, že konečnými lin. kombináciami nedosiahnem celý priestor...
Na druhej strane, vo funkcionálnej analýze sa takáto báza štandardne uvažuje. Hamelova báza hovorí o konečnom nosiči pre každý prvok priestoru, má to s tým súvis?
Prečo algebra pracuje tak často s priamym súčtom a nepáči sa jej priamy súčin?
Offline
#2 25. 08. 2014 11:14 — Editoval Rumburak (25. 08. 2014 13:09)
Re: Báza, modul, priestor ohraničených postupností
↑ kafe_arabica:
Ahoj.
Lebo mám taký pocit, že konečnými lin. kombináciami nedosiahnem celý priestor...
To je správný pocit. :-) Do lineárního obalu (v algebraickém smyslu) množiny
(1) 
patří právě všechny takové posloupnosti, které mají pouze konečný počet nenulových členů.
Existence báze prostoru všech omezených posloupností plyne z axiomu výběru, ale najít nějakou takovou
konkretní jistě nebude triviální (řešení neznám).
Na druhej strane, vo funkcionálnej analýze sa takáto báza štandardne uvažuje.
Můžeš uvést příklad? Myslím, že máš na mysli Schauderovy báze, kde za "lineární kombinaci" připouštíme nejen
konečný součet, ale obecněji i součet konvergentní nekonečné řady (za předpokladu, že na uvažovaném prostoru
je vedle algebraické struktury definována vhodná struktura topologická). Množina (1) je pak Schauderovou bází
prostoru posloupností s konvergentní řadou (pokud se nepletu - už delší dobu jsem se funkcionální analýzou
nezabýval).
Hamelova báza hovorí o konečnom nosiči pre každý prvok priestoru,
Nevím, co máš na mysli pod Hamelovu bazí a konečným nosičem. Mám dojem, že HB je báze, k níž dojdeme,
jestliže daný LP nad tělesem reélných čísel začneme vnímat jako LP nad tělesem racionálních čísel.
Potom každou bázi "nad tělesem reálných čísel" lze rozšířit na Hamelovu bázi "nad tělesem racionálních čísel",
obecně ale ne naopak (protože množina lineárně nezávislá "nad tělesem reálných čísel" je lineárně nezávislá i
"nad tělesem racionálních čísel", ale ne nutně naopak). Souvislost zde proto nevidím .
V té algebraické symbolice se nevyznám.
Offline
#3 25. 08. 2014 19:15
- kafe_arabica
- Příspěvky: 38
- Reputace: 3
Re: Báza, modul, priestor ohraničených postupností
Ďakujem za odpoveď.
Nosičom pre postupnosť  rozumieme množinu
rozumieme množinu  .
.
Nosič je konečný, ak tá množina je konečná.
Hamelova báza pre vektorový priestor V je množina  taká, že je lineárne nezávislá a generuje priestor V, v zmysle:
taká, že je lineárne nezávislá a generuje priestor V, v zmysle:  , kde P je pole, nad ktorým uvažujeme vekt. pr. Pomocou axiómy o výbere sa dá ukázať, že takáto báza existuje pre každý vektorový priestor.
, kde P je pole, nad ktorým uvažujeme vekt. pr. Pomocou axiómy o výbere sa dá ukázať, že takáto báza existuje pre každý vektorový priestor.
Každý vektorový priestor V nad poľom P je aj voľný modul, a teda musí existovať izomorfizmus "u" priestoru V do priestoru  , pričom
, pričom  pre všetky
pre všetky  a
a 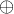 je priamy súčet. Pomocou kanonickej injekcie
je priamy súčet. Pomocou kanonickej injekcie  pre každé iota vytvoríme v priestore
pre každé iota vytvoríme v priestore  bázu a to tak, že pre každé iota zobrazíme jednotku:
bázu a to tak, že pre každé iota zobrazíme jednotku:  .
.
Toto aplikované na konkrétny príklad, ten s postupnosťami, dostaneme:

 , kde 1 na iota-om mieste.
, kde 1 na iota-om mieste.
Tzn., že báza v priestore Post je typu  , ale to je prakticky znova to isté
, ale to je prakticky znova to isté  .
.
A teraz tá záľudná otázka. Táto báza v priestore  stačí, lebo tam sú len postupnosti s konečným nosičom (vďaka priamemu súčtu). Ale táto báza už nestačí v priestore Post.
stačí, lebo tam sú len postupnosti s konečným nosičom (vďaka priamemu súčtu). Ale táto báza už nestačí v priestore Post.
Kde je chyba? Lebo tá báza by mala stačiť aj v priestore Post, čo vyplýva z toho, že Post je voľný modul.
Offline
#4 12. 12. 2014 16:15 — Editoval OiBobik (12. 12. 2014 19:05)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Báza, modul, priestor ohraničených postupností
↑ kafe_arabica:
Ahoj,
co není vidět na první pohled (resp. člověk to tak nějak tuší, ale není vidět skutečně důvod), ale je to pravda, je, že
dimenze  jakožto
jakožto  -lineárního prostoru je nespočetná.
-lineárního prostoru je nespočetná.
Jak na to: stačí najít nějakou nespočetnou, lineárně nezávislou množinu v  .
.
Pro  definujeme
definujeme  . Pak
. Pak  jsou dokonce posloupnosti jdoucí k nule, speciálně jsou omezené, tedy prvky
jsou dokonce posloupnosti jdoucí k nule, speciálně jsou omezené, tedy prvky  .
.
Teď ta jejich lineární nezávislost: konečná lineární kombinace těchto je tvaru  . Předpokládejmě že
. Předpokládejmě že 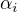 jsou po dvou různá a všechna
jsou po dvou různá a všechna  jsou nenulová reálná čísla. Pak chceme nahlédnout, že
jsou nenulová reálná čísla. Pak chceme nahlédnout, že  .
.
Nechť búno je 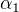 nejmenší z
nejmenší z  Pak
Pak
To by nebylo možné, kdyby  , jelikož
, jelikož  .
.
Našli jsme tedy nespočetnou lineárně nezávislou množinu (dokonce víme i kardinalitu, a to  ). Ta půujde Zornovým lemmatem rozšířit na bázi. Mohutnost této báze, tedy i dimenze, bude nějaké
). Ta půujde Zornovým lemmatem rozšířit na bázi. Mohutnost této báze, tedy i dimenze, bude nějaké  .
.
Tady je vidět chyba ve tvojí úvaze: dimenze  je nespočetná, tedy dokonce není možné mít surjektivní homomorfismus
je nespočetná, tedy dokonce není možné mít surjektivní homomorfismus  .
.
Bude existovat nějaký surjektivní homomorfismus  , ale bude dán stejně ošklivě, jako báze
, ale bude dán stejně ošklivě, jako báze  , tj. nějak "nedostupně" pomocí Zornova lemmatu.
, tj. nějak "nedostupně" pomocí Zornova lemmatu.
EDIT: Teď mě tak napadá, že vlastně je to vidět na první pohled, že dimenze  je nespočetná: Stačí koukat na kardinalidu
je nespočetná: Stačí koukat na kardinalidu  a
a  . Ta první je docela snadno
. Ta první je docela snadno  , kdežto ta druhá je
, kdežto ta druhá je  , jelikož
, jelikož  obsahuje
obsahuje  (dokonce by mělo jít ukázat, že jde o rovnost).
(dokonce by mělo jít ukázat, že jde o rovnost).
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Báza, modul, priestor ohraničených postupností