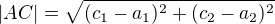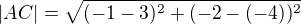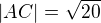Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 05. 04. 2009 12:23
bod na přímce
Zdravím všechny,
mám příklady a nevím co s ním i když vím, že to bude něco velmi jednoduchého:
1)
Na přímce, která prochází body A = [1, 3] a B = [2, 8] leží bod
a) [-2, -11], b) [-1/5, -3], c) [3, 14], d) [4, 19], e) žádným
2)
Uvažujme trojúhelník v rovině o vrcholech
A = [3, -4] a B = [2, -1] C = [-1, -2]
Poloměr krůžnice opsané tomuto trojúhelníku je roven číslu:
a) odmocnina(5), b) odmocnina(10), c) odmocnina(10)/2, d) odmocnina(5)/2, e) žádným
Byl bych moc rád, kdyby mi s nima někdo pomohl, děkuju předem
Offline
#2 05. 04. 2009 12:40
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: bod na přímce
1)
napiš si obecnou rovnici té přímky. Pak dosazuj jeden bod po druhém.
2)
a) složitý postup: udělat dvě osy stran, a vzdálenost jejich průsečíku od jednoho z vrcholů
b) jednoduchý postup: najít vzorec (měl by nějaký být)
Offline
#3 05. 04. 2009 13:37
Re: bod na přímce
↑ Ilias:
Zravím,
add2) Začal bych ověřením, zda trojúhelník není pravoúhlý a on skutečně překvapivě je. Pak už nění žádný problém spočítat poloměr kružnice opsané. Ale pokud by pravoúhlý nebyl, tak bude skutečně nejlepší použít obecnou rovnici kružnice 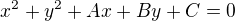 , dosazením tří znamých bodů získáš soustavu tří lineárních rovnic o třech neznámých. Po jejim vyřešení si rovnici kružnice přepíšeš na středový tvar, z kterého zjistíš poloměr.
, dosazením tří znamých bodů získáš soustavu tří lineárních rovnic o třech neznámých. Po jejim vyřešení si rovnici kružnice přepíšeš na středový tvar, z kterého zjistíš poloměr.
*** slovo překvapivě jsem použil, protože předpokládám, že se jedná o příklad z přijímacích testů na VŠE, kde byl zatím vždycky zadán právě trojúhelník pravoúhlý.
Offline
#11 05. 04. 2009 20:36
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: bod na přímce
Ještě pro poloměr opsané kružnice jde použít sinová věta: 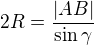
využijeme-li navíc identity pro skalární součin 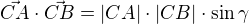
máme hned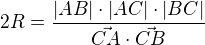
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#12 26. 05. 2009 18:22
Re: bod na přímce
↑ halogan:
u prvního příkladu jsem postupovala podle výše uvedené rady a a dosazovala jsem do obecné rovnice postupně oba body a pokaždé mi vyšlo c=2. Co to ale znamená, jak dál zjistím, která možnost je správná??
Offline
#14 26. 05. 2009 18:38
Re: bod na přímce
↑ Katarina:
Tak to nebylo myšlený :)
Máš body A = [1, 3] a B = [2, 8]
Směrový vektor přímky je teda (1,5) to si převedeš na normálový vektor, což je třeba (-5,1), z toho dostáváš:
-5x+y+c = 0
Tohle ještě ale neni obecná rovnice tý přímky :) musíš zjistit hodnotu toho parametru c a to uděláš tak, že do týhle rovnice dosadíš nějakej bod, kterym ta přímka prochází, takže tam hodíš souřadnice Ačka nebo Bčka a vyjde ti, že c = 2 jak píšeš.
Obecná rovnice tý přímky je teda:
-5x+y+2=0
A do týhle rovnice teprv dosazuješ ty body:
a) [-2, -11], b) [-1/5, -3], c) [3, 14], d) [4, 19]
Offline
#15 26. 05. 2009 18:42 — Editoval xxsawer (26. 05. 2009 18:42)
Re: bod na přímce
↑ gadgetka:
ale notak gadgetko, máš tam chybu :)
No než sem to odeslal tak to bylo fuč :)
Offline
#16 26. 05. 2009 18:44
Re: bod na přímce
Na přímce, která prochází body A = [1, 3] a B = [2, 8] leží bod
a) [-2, -11], b) [-1/5, -3], c) [3, 14], d) [4, 19], e) žádným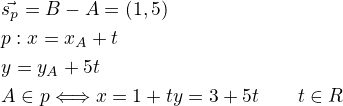
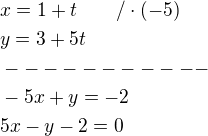
a)
-10+11-2=-1
b)
-1+3-2=0
c)
15-14-2=-1
d)
20-19-2=-1
e)
žádný
b je správně
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
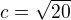 z toho polovina
z toho polovina 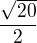 , po usměrnění
, po usměrnění  .
.![kopírovat do textarea $A=[3;-4]$](/mathtex/65/650210dd0639203876274089c7051142.gif)
![kopírovat do textarea $C=[-1;-2]$](/mathtex/50/50d05147c02da6707f708320d21026ca.gif)