Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Definiční obory funkcí - je to dobře? (TOTO TÉMA JE VYŘEŠENÉ)
#2 06. 04. 2009 18:21
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Definiční obory funkcí - je to dobře?
↑ Zbyšek:
1) sinus se nesmí rovnat -sqrt{2}/2, takže 5/4pi a 7/4pi a periody
Navic tangens neni definovan pro nulovy cosinus, takze se nerovna pi/2 plus perioda (jen kpi, bacha)
2) to samé, akorát pro cosinus (3/4pi a 5/4pi)
Offline
#4 06. 04. 2009 18:38 — Editoval joker (06. 04. 2009 18:41)
Re: Definiční obory funkcí - je to dobře?
↑ halogan:
Jej promiň, měl jsem to rozpočítáné a musel jsem jít míchat polívku, tak jsem si po návratu nevšiml, že už jsi sem poslal řešení. Snad se nezlobíš :-)
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Definiční obory funkcí - je to dobře? (TOTO TÉMA JE VYŘEŠENÉ)


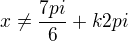
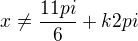
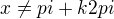
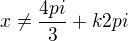
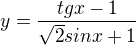
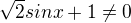
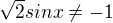
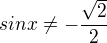
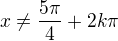
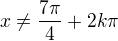
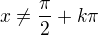
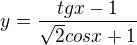
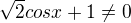
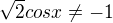
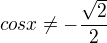
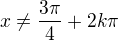
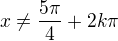
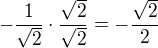 - říká se tomu rozšiřování :-)
- říká se tomu rozšiřování :-)