Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Determinant + matice (TOTO TÉMA JE VYŘEŠENÉ)
#1 20. 10. 2014 14:07
Determinant + matice
Zdravím,
potřebovala bych poradit se dvěma příklady:
1) Užitím úprav, které nemění hodnotu determinantu, spočtěte determinant dané matice řádu n 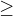 2:
2:
2) Spočítejte inverzní matici k dané matici A řádu n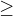 2, je-li
2, je-li
Díky.
Offline
- (téma jako vyřešené označil(a) 188200)
#2 20. 10. 2014 14:23
- OndrasV

- Místo: Praha
- Příspěvky: 513
- Škola: VŠE (1997-2004), FEL (2014-??)
- Pozice: mudrlant
- Reputace: 31
Re: Determinant + matice
↑ 188200: 2) To zvládneš Gaussovou eliminací. Od prvního řádku odečteš a*druhý řádek,
od druhého a*třetí, od a*(n-1)tého a*n-tý a tak se zbavíš mocnic a nad diagonálou.
1) ke každému řádku přičteš první a dostaneš trojúhelníkovou matici s prvkem 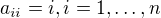 , tj. determinant je součet prvků na diagionále, tj.
, tj. determinant je součet prvků na diagionále, tj.  .
.
Offline
#3 20. 10. 2014 17:38
Re: Determinant + matice
Pozdravujem,
2)
Stoji za to napisat tvoju maticu ako sucet diagonalmych matic.
Oznacme tu nad hlavnou diagonalov ( ta co ma same a) N.
Co mozes o nej provedat?
Vyuzi to!
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Determinant + matice (TOTO TÉMA JE VYŘEŠENÉ)
