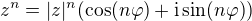Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 21. 10. 2014 18:13
- janca361

- .
- Příspěvky: 3284
Re: Goniometrie
↑ Sheldon.C:
Je moc velký problémurčit hodnoty 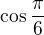 a
a  . Měl by si to vědět z hlavy, pokud nevíš, použil kalkulačku.
. Měl by si to vědět z hlavy, pokud nevíš, použil kalkulačku.
Offline
#3 21. 10. 2014 18:16
Re: Goniometrie
Ahoj,
komplexní číslo lze zadat algebraicky: V gaussově rovině to znamená bod [a;b]
V gaussově rovině to znamená bod [a;b]
V gaussove rovině však lze bod definovan i jinak než vypsáním souřadnic a to pomocí úhlu sevřeného s kladnou x-ovou poloosou a vzdálenosti bodu do nuly.
Pro komplexní číslo ve tvaru  platí
platí
kde fi je úhel sevřený s kladnou poloosou.
Vzdálenost bodu od počátkou souřadnic [0;0] nám určuje absolutní hodnota. V pravoúhlém trojúhelníku je přeponou právě tato vzdálenost |z|, horizontální odvěsna je "a" a vertikální odvěsna je "b"
Z definice sinu a kosinu lze tedy psát:
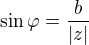
Řešíš tedy soustavu dvou rovnic sice o jedné neznáme, ale jelikož sinus i kosinus jsou periodické funkce, tak vzikají i výsledky "navíc". Nás zajímá právě ten, kdy se budou dané úhly rovnat.
S touto znalostí lze pak přepisovat goniometrický tvar na algebraický a naopak.
Ve tvém případě však bohatě postačí, když kosinus i sinus vyjádříš a jednoduše roznásobíš závorku.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#7 21. 10. 2014 18:53 — Editoval misaH (21. 10. 2014 18:59)
- misaH
- Příspěvky: 13459
Re: Goniometrie
↑ Sheldon.C:
Miesto n napíš trojku.
Miesto AH z napíš 2.
Fí je pí/6.
Prečo "riešiš" takéto úlohy?
Bez teórie je to škoda času.
Táto úloha sa dá riešiť úplne spamäti, treba si iba pozrieť najzákladnejšiu teóriu. Nastínil ju Freedy.
Offline
#8 22. 10. 2014 10:55
- petrik_ch

- Místo: Topoľčany
- Příspěvky: 242
- Škola: ZS Tribecska Topolcany
- Pozice: priatel skoly, absolvent, rodic
- Reputace: 2
- Web
Re: Goniometrie
pi/6 = 30 stupnov;
Je to toto komplexne cislo 2L30 (zadane vo verzorovom tvare):
http://www.hackmath.net/cz/kalkulacka/k … p;submit=1
Offline