Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 27. 12. 2014 11:28
#5 27. 12. 2014 13:20 — Editoval Rufus (27. 12. 2014 13:21)
Re: Vyjádření neznámé
↑ holyduke: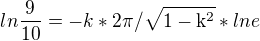
takže to 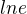 tam mám správně ano? Právě jsem si nebyl jistý, zda tam nezůstane jenom:
tam mám správně ano? Právě jsem si nebyl jistý, zda tam nezůstane jenom: 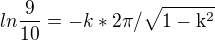
Pokračuju takto. Je to dobře? Pokud ano, tak už ale nevím jak dál...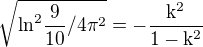
Offline
#10 27. 12. 2014 17:52 — Editoval misaH (27. 12. 2014 22:04)
- misaH
- Příspěvky: 13460
Re: Vyjádření neznámé
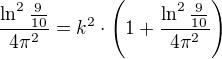
Deleno zátvorka na pravej strane
Upraviť (ak sa dá)
Odmocniť
Podmienky uvážiť.
Nekontrolovala som nič.
OT:
To ste dajako náročná základná škola - moderátori asi nevedia, čo sa učí na ZŠ, už to tak vyzerá.
Hlavne že sú určené na fóre kategórie a že sa "nahlasuje".
Offline
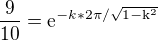

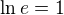
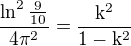
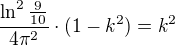
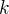 dať na jednu stranu
dať na jednu stranu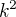
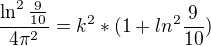 ?
?