Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » dvourozměrné rozdělení pravděpodobnosti - střední hodnoty
#1 27. 12. 2014 19:53
- marapech@gmail.com

- Zelenáč
- Příspěvky: 1
- Škola: UHK
- Reputace: 0
dvourozměrné rozdělení pravděpodobnosti - střední hodnoty
Dobrý den, mám menší problém s příkladem z učebnice Rozhodování při riziku (Petr Hebák).
V učebnici není o dvourozměrných rozděleních ani zmínka a z internetových zdrojů jsem nebyl schopen pochopit jak na to.
Prosím Vás tedy o pomoc. Snad mi bude stačit jen navedení jakou cestou se do toho pustit :)
Offline
#2 28. 12. 2014 05:37
- seliga.adam
- Zelenáč
- Příspěvky: 12
- Reputace: 1
Re: dvourozměrné rozdělení pravděpodobnosti - střední hodnoty
Stredného hodnoty vypočítaš tak, že sa pozrieš na marginálne pravdepodobnosti. Napríklad, keď rátaš strednú hodnotu náhodnej premennej  , tak
, tak  nadobudne hodnotu
nadobudne hodnotu  s pravdepodobnosťou
s pravdepodobnosťou 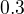 , hodnotu
, hodnotu  s
s  a hodnotu
a hodnotu  s
s 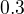 . Vypočítaš strednú hodnotu rovnako ako pri jednorozmernej náhodnej premennej, teda:
. Vypočítaš strednú hodnotu rovnako ako pri jednorozmernej náhodnej premennej, teda:
Podobne vypočítaš strednú hodnotu pre 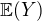 , ktorá je v tomto prípade rovnaká.
, ktorá je v tomto prípade rovnaká.
Takisto postupuješ aj pri rozptyle.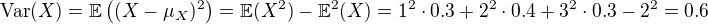
Rovnako aj pri variancii premennej  .
.
Podobne vypočítaš aj kovarianciu.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » dvourozměrné rozdělení pravděpodobnosti - střední hodnoty