Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 31. 12. 2014 14:30
- Argcotgh x
- Příspěvky: 230
- Škola: MFF UK
- Pozice: student
- Reputace: 5
Integrál (racionální funkce)
Zdravím, mám problém s integrálem.
Zadání: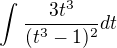
Řešení: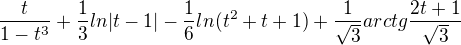
Všechny členy řešení mi vycházejí, až na první - integrál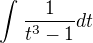
Který se má rovnat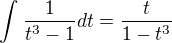
Možná že je triviální, ale nedaří se mi na něj přijít. Mohu poprosit o pomoc? Předem díky.
Offline
#2 31. 12. 2014 15:59
Re: Integrál (racionální funkce)
↑ Argcotgh x:
Dobrý den.
Řekl bych, že neplatí 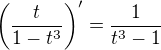 , takž ve výpočtu je zřejmě něco v nepořádku.
, takž ve výpočtu je zřejmě něco v nepořádku.
Pokud se tedy nemýlím.
Online
#3 31. 12. 2014 16:03
- Argcotgh x
- Příspěvky: 230
- Škola: MFF UK
- Pozice: student
- Reputace: 5
Re: Integrál (racionální funkce)
Dobrý den, děkuji za podpoření, taky jsem to zkoušel derivovat a nevycházelo to. Nevím však, jak na ten integrál - nenapadá mě rozumná substituce, která by tam nepřidala člen navíc.
Offline
#4 31. 12. 2014 17:04
- tomas janeta
- Příspěvky: 67
- Škola: gymnázium antona bernoláka námestovo
- Pozice: študent
- Reputace: 5
Re: Integrál (racionální funkce)
Dobrý ,možno sa mýlim ale nemohla by to byť 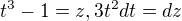 .
.
Ak sa mýlim prepáčte ,som prvák na strednej
Offline
#5 31. 12. 2014 17:12
- Argcotgh x
- Příspěvky: 230
- Škola: MFF UK
- Pozice: student
- Reputace: 5
Re: Integrál (racionální funkce)
To právě nejde, v integrandu mi "chybí" ten člen 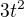 , abych mohl použít tuhle substituci.
, abych mohl použít tuhle substituci.
Offline
#6 31. 12. 2014 17:28
- tomas janeta
- Příspěvky: 67
- Škola: gymnázium antona bernoláka námestovo
- Pozice: študent
- Reputace: 5
Re: Integrál (racionální funkce)
Prepáčte ,pred chvíľou som chybu zbadal sám .Integrovať sa ešte len učím... ,ešte raz prepáčte
Offline
#7 31. 12. 2014 17:30
Re: Integrál (racionální funkce)
↑ Argcotgh x: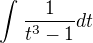 je pořád racionální funkce. Pokud tě nenapadá jiná možnost, rozlož jí na parciální zlomky...
je pořád racionální funkce. Pokud tě nenapadá jiná možnost, rozlož jí na parciální zlomky...
Offline
#8 31. 12. 2014 18:59 — Editoval Jj (31. 12. 2014 19:00)
Re: Integrál (racionální funkce)
↑ Argcotgh x:
Řekl bych, že se tam objevila chybka už někde v průběhu výpočtu.
Když s pomocí WA rozložím integrand na parciální zlomky a zintegruju jednolivé výrazy, dostanu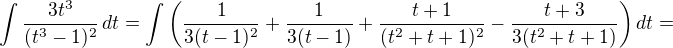
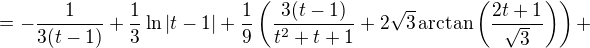
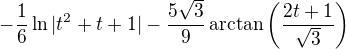
Po úpravě: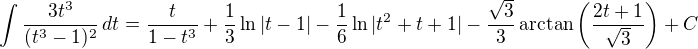
což by měl být výsledek (derivace to potvrzuje).
Pokud se tedy nemýlím.
Online
#9 31. 12. 2014 19:57
- Argcotgh x
- Příspěvky: 230
- Škola: MFF UK
- Pozice: student
- Reputace: 5
Re: Integrál (racionální funkce)
Asi jsem udělal chybu už v parciálních zlomcích. Ale stále mi není jasný ten člen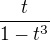
Offline
#11 31. 12. 2014 20:16
- Argcotgh x
- Příspěvky: 230
- Škola: MFF UK
- Pozice: student
- Reputace: 5
Re: Integrál (racionální funkce)
Ano, když jsem to teď sečetl, skutečně to dalo ten podivný člen. Díky moc!
Offline

