Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 05. 01. 2015 20:14
- terezkaaaaa5

- Příspěvky: 1221
- Reputace: 2
Lokální extrémy
Dobrý den, pomůžete mi prosím s tímto příkladem?
Mám funkci f(x) = 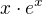 a mám určit lokální extrémy, kdy je funkce klesající a rostoucí.
a mám určit lokální extrémy, kdy je funkce klesající a rostoucí.
Derivace funkce mi vyšla 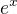 , ale dále už nevím, co s tím. díky za pomoc.
, ale dále už nevím, co s tím. díky za pomoc.
Offline
#2 05. 01. 2015 20:24
Re: Lokální extrémy
↑ terezkaaaaa5:Ahoj, ta derivacia ale nie je dobre. Pozri sa ako vyzera derivacia sucinu dvoch funkcii.
Offline
#4 05. 01. 2015 20:31
Re: Lokální extrémy
↑ terezkaaaaa5:To je uz lepsie. No a nakolko ta o chvilku bude zaujimat jej znamienko, odporucam napisat si ju v tvare  .
.
Offline
#5 05. 01. 2015 20:31
- terezkaaaaa5

- Příspěvky: 1221
- Reputace: 2
Re: Lokální extrémy
↑ vlado_bb:
dobře díky. A co dál prosím?
Offline
#6 05. 01. 2015 20:32
#7 05. 01. 2015 20:35
- terezkaaaaa5

- Příspěvky: 1221
- Reputace: 2
Re: Lokální extrémy
↑ vlado_bb:
Vždy jsem postupovala podle řešených příkladů na hodinách. Tam jsme určovali D(f) a nulové body. Taty ale takové body nejsou
Offline
#8 05. 01. 2015 20:39
Re: Lokální extrémy
↑ terezkaaaaa5:Treba studovat podla nejakej knihy, inak to nestoji za nic.
Offline
#9 05. 01. 2015 20:45
- terezkaaaaa5

- Příspěvky: 1221
- Reputace: 2
Re: Lokální extrémy
↑ vlado_bb:
To už mi došlo také, jenže teď už toto asi nedoženu. Ještě jsem zjistila chybku v zadání, kdy  Bude to tedy:
Bude to tedy: 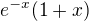 . A prosím poradíte mi co dále?
. A prosím poradíte mi co dále?
Offline
#10 05. 01. 2015 20:51
Re: Lokální extrémy
↑ terezkaaaaa5:Terazka, rad by som ti pomohol, ale bolo by to porusenim zasad tohoto fora. Mam na mysli zasadu, podla ktorej ma zadavatel otazky preukazat istu snahu ulohu vyriesit samostatne. A ak si niekto ani len nezaobstara prislusnu literaturu, nemoze sa podla mna hovorit o splneni tejto zasady.
Offline
#11 05. 01. 2015 21:03
- terezkaaaaa5

- Příspěvky: 1221
- Reputace: 2
Re: Lokální extrémy
↑ vlado_bb:
Při hledání nulových bodů se zderivovaná funkce dává rovno nule, exponenciála se ale nule rovnat nemůže. Proto nevím jak pokračovat a ať hledám, kde hledám, nemůžu nic najít
Offline
#12 05. 01. 2015 21:09 — Editoval byk7 (05. 01. 2015 21:11)
Re: Lokální extrémy
↑ terezkaaaaa5: exponenciela sama o sobě nule rovna nebude, ale máš tam ještě ten druhý činitel :-)
Ale ta derivace je nyní špatně, zkus se na ni ještě podívat.
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#13 05. 01. 2015 21:11
- terezkaaaaa5

- Příspěvky: 1221
- Reputace: 2
Re: Lokální extrémy
↑ byk7:
Takže když se x = -1. to tedy bude jediný nulový bod a podle toho si rozdělím intervaly na (-nek;-1), -1 , (-1;nek.)? :)
Offline
#14 05. 01. 2015 21:45
Re: Lokální extrémy
↑ terezkaaaaa5:
Už jsem psal, že ta tvá ↑ derivace: je špatně. Oprav si to a dál postupuj tak, jak jsi zvyklá a naučená. :-)
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#15 05. 01. 2015 21:51
- terezkaaaaa5

- Příspěvky: 1221
- Reputace: 2
Re: Lokální extrémy
↑ byk7:
Derivaci tedy není:  ? Tak v tom případě nevím, kde mám chybu
? Tak v tom případě nevím, kde mám chybu
Offline
#16 05. 01. 2015 21:55
Re: Lokální extrémy
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#17 05. 01. 2015 21:57
- terezkaaaaa5

- Příspěvky: 1221
- Reputace: 2
Re: Lokální extrémy
↑ byk7:
Ale derivace exponenciály je přece to samé. Nebo ne?
Offline
#18 05. 01. 2015 22:02 Příspěvek uživatele Freedy byl skryt uživatelem Freedy. Důvod: nepozorný :D
#19 05. 01. 2015 22:02 — Editoval byk7 (05. 01. 2015 22:03)
Re: Lokální extrémy
↑ terezkaaaaa5:
No, ne úplně přesně, ano platí 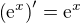 , ale pro
, ale pro  už rovnost
už rovnost  neplatí.
neplatí.
A ty hledáš derivaci funkce 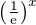 :-)
:-)
↑ Freedy: -> ↑ terezkaaaaa5: ;-)
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#21 05. 01. 2015 22:06 — Editoval Freedy (05. 01. 2015 22:24)
Re: Lokální extrémy
byk7 napsal(a):
, ale pro
už rovnost
neplatí.
↑ Freedy: -> ↑ terezkaaaaa5: ;-)
a co kdyby pro  bylo
bylo 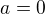 ? tak to také neplatí? ;)
? tak to také neplatí? ;)
↑ terezkaaaaa5:
Jak je definována derivace funkce  ?
?
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#22 05. 01. 2015 22:34
- terezkaaaaa5

- Příspěvky: 1221
- Reputace: 2
Re: Lokální extrémy
↑ Freedy: Ale v tomhle konkrétním příkladě si prostě nevím rady. Díky za váš čas, ale bohužel to teď nedokážu vymyslet.
Ale v tomhle konkrétním příkladě si prostě nevím rady. Díky za váš čas, ale bohužel to teď nedokážu vymyslet.
Offline
#23 05. 01. 2015 23:07
Re: Lokální extrémy
↑ Freedy: Pán je hnidopich, co? :-D Samozřejmě, že uvažujeme "klasickou" exponenciální funkci, tj.  .
.
↑ terezkaaaaa5: Tak si tam dosaď 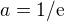 , kolik je
, kolik je  ?
?
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline

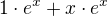

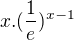 ?
?