Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 14. 01. 2015 19:38
- miluska535
- Příspěvky: 41
- Reputace: 0
Centrální limitní věta
Pojišťovna pojišťuje 5000 lidí stejného věku. Pravděpodobnost úmrtí během roku je 0,002. Každý pojištěnec zaplatí 2500 Kč. V případě úmrtí vyplatí rodině 1 000 000 Kč. Jaká je pravděpodobnost, že pojišťovna utrpí ztrátu? Použijte CLV.
Mohl by mi někdo poradit aspoň začátek tohoto příkladu? Vůbec nevím, jak mám začít...děkuji.
Offline
#2 16. 01. 2015 19:30
Re: Centrální limitní věta
↑ miluska535:
Dobrý večer.
X - počet zemřelých za rok (z počtu 5000 pojištěnců) - náhodná veličina s binomickým rozložením
pravděpodobnosti (Odkaz) s p = 0.002, n = 5000 se střední hodnotou a rozptylem:

Pojištění celkem činí 12500000 Kč. Pokud bude možno předpokládat, že prodělávat bude pojišťovna při
počtu úmrtí >= 13/rok, tak je třeba zjistit pravděpodobnosti P(X >12).
Podle CLV lze hledanou pravděpodobnost přibližně určit pomocí distribuční funkce F(x) normálního rozložení .
.
Pokud se tedy nemýlím.
Offline
#3 11. 02. 2019 11:32
Re: Centrální limitní věta
Ahoj, mám stejný příklad, proto to vkládám do tohoto vlákna.
a) určete střední hodnotu a směrodatnou odchylku plateb vztahující se k jednomu pojištěnci.
X...náhodná veličina udávající platbu jednoho pojištěnce


b) Určete rozdělení plateb pro všechny pojištěnce dohromady - Tady tápu
X...náhodná veličina udávající počet zemřelých za rok
Potom rozdělění plateb pro všechny pojištěnce dohromady bude 
Děkuji za rady
Offline
#4 13. 02. 2019 13:57 — Editoval Jj (13. 02. 2019 14:01)
Re: Centrální limitní věta
↑ žabí hněv:
Zdravím. Ze zadání úlohy ↑ miluska535: soudím, že se jedná o platby za jeden rok.
X ... platby pojišťovny při úmrtí pojištěnce - náhodná proměnná
Y ... celkem platby při jednom pojištěnci
Pojišťovna vyplatí rodině: 0 Kč s P = 0.998
1000000 Kč s P = 0.002


Konstantní platba pojištěnce = 2500 Kč (ta jen "posune" E(X), rozptyl a směrodatnou odchylku neovlivní). Takže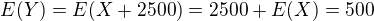

Rozdělení za všechny ~ řekl bych, centrální limitní věta.
Poznámka: Je přece jen rozumnější založit pro každý dotaz nové téma. Jinak se dotaz lehce přehlédne.
Pokud se tedy nemýlím.
Offline
