Matematické Fórum

lucka14lucky · 20. 01. 2015 21:02

Prosím o návod na příklad. Nevysvětlil by jste mi někdo, co mám počítat? Moc tomu nerozumím. Když chtějí délku lana, tak jakoby dráhu že ano? Jenže to lano se mi navíjí na sebe, takže po každé je jakoby ten kruh jinak velký.. Nebo to je špatná úvaha?

//forum.matweb.cz/upload3/img/2015-01/84020_20150120_202453.jpg

o.neill · 23. 01. 2015 15:13

No, myslím, že to chápeš správně. Tloušťku lana, a tedy zvětšování průměru je dle mého možné zanedbat. Ale stejně se mi ten příklad zdá zadaný nějak blbě. Zdá se mi, že aby se vyřešil ten průběh toho navíjení, je potřeba vyřešit nelineární diferenciální rovnici druhého řádu, která pokud vím nemá řešení v analytickém tvaru. Navíc tam vůbec nejsou specifikovány žádné počáteční podmínky. K tomu nesedí rozměr té konstanty A, která by tam měla mít sekundu na druhou.

Ještě mě teď napadlo, že se to vlastně možná myslí tak, že to zrychlení neroste kontinuálně, ale vždycky poskočí, když se provede jedna otáčka. Stále sice má to A špatné jednotky, ale asi to aspoň jde nějak vyřešit. Nicméně mně to stejnak moc v souladu s výsledky nevychází.

Jj · 23. 01. 2015 17:35

Zdravím ↑ o.neill:

Já jsem v jiném tématu kolegyni ↑ lucka14lucky: slíbil, že se na tento příklad podívám. Možná něco v zadání přehlížm, ale zatím mi zadání taky připadá nějak neúplné. Řekl bych, že zrychlení je zadáno jako kontinuální, že nelineárnost rovnice obecně neznamená nemožnost řešení v analytickém tvaru. Z matných vzpomínek na kinematiku jsem se snažil k něčemu rozumnému dojít, ale v řešení mi zatím vždycky "něco chybí" a z uvedených výsledků úloh se mi zatím nepodařilo "uhádnout", co asi.

Možná by prospělo, kdyby si úlohy všiml kolega "zdenek1", který ve fyzice vyřeší kde co.

o.neill · 23. 01. 2015 19:21

Zdravím, nelineárnost sice obecně neznamená nemožnost analytického řešení, ale podle WolframAlpha je řešením této rovnice jakási Weierstrassova eliptická funkce. Navíc nejsou-li určeny počáteční podmínky, můžem jenom hádat, jestli mají být φ(0)=0 a ω(0)=0, pak je otázka, jestli vůbec existuje nějaké nenulové řešení té dif. rce (hádal bych že ne, wolfram to z nějakého důvodu nespočítá s těmito počátečními podmínkami).

jelena · 23. 01. 2015 20:17

Zdravím,

to jsme už celkem velká sestava :-) Kousek úlohy jsme diskutovali v tématu, ale potom jsem zkoušela rozepsat řešení a nic nevzešlo.

Zkoušela jsem uvažovat i složenou funkci 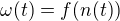$\omega(t)=f(n(t))$ i slovo "max" jakože průběh obvodové rychlosti má maximum. A nic. Počáteční podmínky bychom mohli používat, že pro t=0 je všechno 0, ale ani tak (n se dostalo do jmenovatele po integrování, tedy nulové být nemůže). Ještě možný překlep N^(-2) v zadání?

Pokud vezmeme druhý vztah z výsledku a dosadíme za $l$ jeden obvod bubnu, nenavede to? Nebo úplně poslední vztah - je to cca 1 obvod bubnu, který se navine za posledních 2,5 s.

No úloha je to podnětná, ale mně to moc nemyslí ani na méně podnětné -máme nějak pracovně moc a doma je období olympiád. Tak vás budu průběžně pozorovat.

Brzls · 24. 01. 2015 10:41

↑ o.neill:
Zdravím
Jen poznámka - jestli dobře chápu, že 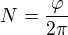$N=\frac{\varphi }{2\pi }$ kde fí je prostě o kolik radiánů se od začátku buben otočil, tak ta rovnice řešitelná je

Je ve tvaru
$\frac{\mathrm{d^{2}}\varphi }{\mathrm{d}t^{2} }-k\varphi ^{2}=0$
Zkusíme najít nějakou zachovávající se veličnu. Zkusíme celou rovnici vynásobit derivací fí a po integraci dostaneme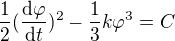

$\frac{1}{2}(\frac{\mathrm{d} \varphi }{\mathrm{d} t})^{2}-\frac{1}{3}k\varphi ^{3}=C$
kde C je první integrační konstanta. KDyž nyní uvážíme, že s počtem vykonaných otáček roste úhlové zrychlení, měla by růst i úhlová rychlost. Tím pádem můžeme vyjádřít první derivaci fí a separovat proměnné.

Mimochodem když se to dořeší tak je to i odpověď na otázku proč to wolfram nespočítá když se jako podmínky v čase t=0 všechno položí rovno nule.

Co se týče příkladu samotného, tak je prostě nejednoznačně zadaný. Možná by šlo právě zkusit udělat obecné řešení rovnice a zkusit seštelovat počáteční podmínky tak, aby seděli výsledky (zkoumat jeslti je to vůbec možné atd.)

Jj · 24. 01. 2015 12:24

Zdravím ↑ Brzls:

O to seštelování podmínek jsem se už snažil. Zatím nic moc. Bude-li čas, ještě se k tomu vrátím.

Zdravím i kolegyni ↑ jelenu:, nějak jsem přehlédl, že v tématu podle odkazu ještě diskuse pokračovala. Snad se k něčemu dopídíme.

o.neill · 25. 01. 2015 09:34

Aha, tak akorát neumím řešit diferenciální rovnice. Nicméně teď teda hledáme řešení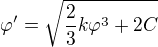
$\varphi'=\sqrt{\frac{2}{3}k\varphi^3+2C}$ , že?
Pak už jsme to teda dopočítali, ne? Až na to samozřejmě, že neznáme ty počáteční podmínky. A hledat integrační konstanty tak, aby φ(0)=0 a φ'(0)=0 je podle mého marná snaha. Dosazením do té dif. rce je vidět, že aby byly splněny obě tyto poč. podmínky, musí být C=0. Řešíme pak
$\varphi'=\sqrt{2k/3}\varphi^{3/2}$
pravá strana této rovnice je Lipschitzovská, takže pro poč. podmínku φ(0)=0 existuje právě jedno řešení. Toto řešení je nulová funkce.

Matematické Fórum

#1 20. 01. 2015 21:02

Kruhový pohyb

#2 23. 01. 2015 15:13

Re: Kruhový pohyb

#3 23. 01. 2015 17:35

Re: Kruhový pohyb

#4 23. 01. 2015 19:21

Re: Kruhový pohyb

#5 23. 01. 2015 20:17

Re: Kruhový pohyb

#6 24. 01. 2015 10:41

Re: Kruhový pohyb

#7 24. 01. 2015 12:24

Re: Kruhový pohyb

#8 25. 01. 2015 09:34

Re: Kruhový pohyb

Zápatí