Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Riemannov integrál (TOTO TÉMA JE VYŘEŠENÉ)
#1 24. 04. 2009 00:28
Riemannov integrál
Ahojte,
zaujímalo by ma, akým spôsobom by ste dokazovali nasledovné tvrdenie:
Nech ![kopírovat do textarea $f\,:\;[a,b]\to\mathbb{R}$](/mathtex/84/84aee82a1a124ea58aea360aee92f471.gif) je spojitá nezáporná funkcia, tak
je spojitá nezáporná funkcia, tak![kopírovat do textarea $\lim_{n\to\infty}\(\int_{a}^{b}f^n(x)\,\rm{d}x\)^{1/n}=\max_{x\in[a,b]}f(x).$](/mathtex/f7/f7044328f132d77c3a5423c0893702a6.gif)
Nie som si celkom istý určitým krokom, svoje by som pridal neskôr aby som neovplyvňoval. Aj tak to bude asi zle :-)
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#2 24. 04. 2009 10:14 — Editoval Rumburak (24. 04. 2009 10:45)
Re: Riemannov integrál
Označme ![kopírovat do textarea $m=\max_{x\in[a,b]}f(x)$](/mathtex/0f/0fc462fc82dc084afbd869cdf161374d.gif) . Pokud je m=0, Tvůt vzorec je splněn triviálně. Nechť nadále
. Pokud je m=0, Tvůt vzorec je splněn triviálně. Nechť nadále  . Položme
. Položme  pro
pro ![kopírovat do textarea $x\in [a,b]$](/mathtex/18/18b9398de5e89cbd388d1c85889089d8.gif) .
.
Funkce g je na uvedeném intervalu spojitá, pro každé x je 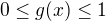 , přičemž v jistém
, přičemž v jistém ![kopírovat do textarea $c\in [a,b]$](/mathtex/d0/d080b34a4e1f20774e0ac693be694086.gif) je
je 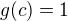 . Dokazovaná rovnost
. Dokazovaná rovnost
pak je ekvivalentní s rovností .
.
Zvolme  . Existuje množina
. Existuje množina ![kopírovat do textarea $M_h\subseteq [a,b] $](/mathtex/b0/b0c7e81ddc614ee34d33916026848037.gif) kladné míry taková, že pro každé
kladné míry taková, že pro každé  je
je  . Potom
. Potom , takže
, takže![kopírovat do textarea $h \sqrt[n]{\mu(M_h)} \le \sqrt[n]{\int_{a}^{b}g^n(x)\,\rm{d}x\ } \le \sqrt[n]{b-a} $](/mathtex/5c/5cc2be645b8a0f6905fdf4330eac3148.gif) ,
,
na tuto nerovnost provedeme limitu a dostaneme![kopírovat do textarea $h \le \liminf_{n \to \infty} \sqrt[n]{\int_{a}^{b}g^n(x)\,\rm{d}x\ } \le 1 $](/mathtex/89/89b1c760f77f33dfd748735ab43c40b0.gif) .
.
Poslední nerovnost platí pro libovolné h < 1 , takže liminf je limitou rovnou 1 (že limsup je také <= 1 , je zřejmé).
Offline
#3 24. 04. 2009 10:49
Re: Riemannov integrál
↑ Rumburak:
Ahoj, nerozumiem dobre, čo myslíš pod  .
.
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#4 24. 04. 2009 10:58
Re: Riemannov integrál
↑ lukaszh:
Ahoj taktéž,
myslím tím Lebesgueovu míru množiny M_h (nechtěl jsem se patlat s nějakými "deltami", tak jsem využil skutečnosti,
že Riemannův integrál je Lebesgueovým integrálem). Jinak pod M_h si můžeš představit interval kladné délky a
číslo  touto délkou.
touto délkou.
Offline
#5 24. 04. 2009 10:59
Re: Riemannov integrál
↑ Rumburak:
Ďakujem, v tom prípade chápem. Celkom šikovné :-)
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Riemannov integrál (TOTO TÉMA JE VYŘEŠENÉ)
