Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 09. 03. 2015 14:36 Příspěvek uživatele byk7 byl skryt uživatelem byk7.
#7 09. 03. 2015 18:22
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Derivace 1 a 2..
Zdravím,
↑ autor tématu: pokud je X poloha těžiště závislá na čase, potom předpokládám, že 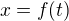 ,
, 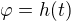 . Při derivování po dt uvažuješ složené funkci a tak derivuješ. Pro 2. derivaci je třeba brát ohled jak na složenou funkci, tak i na derivování součinů.
. Při derivování po dt uvažuješ složené funkci a tak derivuješ. Pro 2. derivaci je třeba brát ohled jak na složenou funkci, tak i na derivování součinů. je na
je na  patrně nezávislé, tedy považuješ za konstantu (stejně tak, jako
patrně nezávislé, tedy považuješ za konstantu (stejně tak, jako 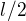 ). Pro získaní výsledku Tobě by mělo stačit jen opisovat vzor co máš a na příslušných místech nahrazovat
). Pro získaní výsledku Tobě by mělo stačit jen opisovat vzor co máš a na příslušných místech nahrazovat  za
za 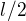 . Ovšem v tom vzoru vidím drobné chyby (snad ale jen u derivování
. Ovšem v tom vzoru vidím drobné chyby (snad ale jen u derivování 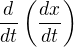 . Pokud potřebuješ princip derivování, tak trochu podrobněji viz úvod mého příspěvku a ozvi se, prosím, zda stačilo. Děkuji.
. Pokud potřebuješ princip derivování, tak trochu podrobněji viz úvod mého příspěvku a ozvi se, prosím, zda stačilo. Děkuji.
Offline
#11 09. 03. 2015 20:46
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Derivace 1 a 2..
derivoval jsi všechno podle času, výsledek derivování jsi zapsal, derivace  je derivace složené funkce, proto máš derivaci vnější funkce
je derivace složené funkce, proto máš derivaci vnější funkce  * derivace vnitřní funkce
* derivace vnitřní funkce 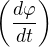 . Tak můžeš pokračovat k 2. derivaci.
. Tak můžeš pokračovat k 2. derivaci.
Offline
#14 09. 03. 2015 22:14
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Derivace 1 a 2..
:-) krasopis je základ pro technika. Správně.
Kopíruješ i drobnou chybu: z 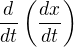 má být
má být 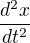 - viz zápis pro vyšší derivaci v odkazu (toto je "čistá druhá" derivace).
- viz zápis pro vyšší derivaci v odkazu (toto je "čistá druhá" derivace).
Potom 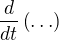 je operátor, který nařizuje derivaci toho, co je v závorce, tedy mezi operátorem a závorkou nemůže být znak násobení (4. řádek na 2. papíře). Stejně tak do závorky zapíšeme
je operátor, který nařizuje derivaci toho, co je v závorce, tedy mezi operátorem a závorkou nemůže být znak násobení (4. řádek na 2. papíře). Stejně tak do závorky zapíšeme 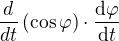 , derivujeme jen cos, násobíme druhou funkci nederivovanou, jelikož derivujeme součin (pokračování nebudu vypisovat, je v pořádku).
, derivujeme jen cos, násobíme druhou funkci nederivovanou, jelikož derivujeme součin (pokračování nebudu vypisovat, je v pořádku).
Je jasné jak z 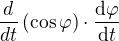 vzniklo
vzniklo 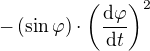 ? Které Ty ovšem nemáš oproti vzoru. Je totiž rozdíl mezi
? Které Ty ovšem nemáš oproti vzoru. Je totiž rozdíl mezi 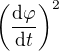 , které vzniká jako násobení 2 prvních derivací a
, které vzniká jako násobení 2 prvních derivací a 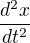 , což odpovídá jedné druhé derivaci.
, což odpovídá jedné druhé derivaci.
Tak ještě poopravuj, děkuji.
Offline
#18 09. 03. 2015 22:57
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Derivace 1 a 2..
↑ příspěvek 16: v kroužku je v pořádku a závěr také, můj předchozí příspěvek byl ještě před novým papírem
Offline
#20 10. 03. 2015 00:01
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Derivace 1 a 2..
↑ příspěvek 19: pokud jsem nic nepřehlédla, tak v pořádku, jen úplně na začátku pro 2. derivaci nalevo má být 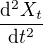
Offline



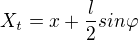 není jasné, jak tato funkce závisí na proměnné
není jasné, jak tato funkce závisí na proměnné 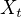 jako
jako 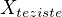 .. nic jineho v tom není ..
.. nic jineho v tom není ..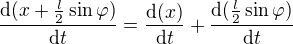
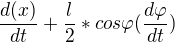 .. ..takže v podstatě jsem derivoval jen to sinus podle času
.. ..takže v podstatě jsem derivoval jen to sinus podle času


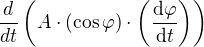 , konstanta A jde před derivaci, derivuješ součin a dál máš rozepsáno
, konstanta A jde před derivaci, derivuješ součin a dál máš rozepsáno 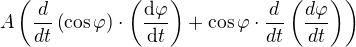
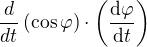 je třeba zapsat pořádně.
je třeba zapsat pořádně.