Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » určitý integrál per partes (TOTO TÉMA JE VYŘEŠENÉ)
#1 04. 04. 2015 15:48
- 126Magdaléna126

- Příspěvky: 30
- Reputace: 0
určitý integrál per partes
Prosím o pomoc s týmto príkladom :prosím o podrobné vysvetlenie ďakujem


Offline
- (téma jako vyřešené označil(a) jelena)
#2 04. 04. 2015 16:49 — Editoval Freedy (04. 04. 2015 17:06)
Re: určitý integrál per partes
Ahoj,
určitý integrál pomocí per partes vypadá následovně:![kopírovat do textarea $\int_{a}^{b}f(x)g'(x)\text{dx}=[f(x)g(x)]_a^b-\int_{a}^{b}f'(x)g(x)\text{dx}$](/mathtex/c3/c31fb1130bc2dc842ec84a70a6e6602b.gif)
ty máš integrál 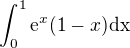 vzhledem k tomu, že máš dvě možnosti - derivovat buď e^x nebo (1-x), si vybereš nejspíš derivování (1-x) protože to se po zderivování zjednoduší.
vzhledem k tomu, že máš dvě možnosti - derivovat buď e^x nebo (1-x), si vybereš nejspíš derivování (1-x) protože to se po zderivování zjednoduší.
Stačí tedy položit 
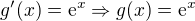
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#3 04. 04. 2015 17:03
- 126Magdaléna126

- Příspěvky: 30
- Reputace: 0
Re: určitý integrál per partes
↑ Freedy:
teda aký bude výsledok?
ďakujem :)
Offline
#5 04. 04. 2015 17:14
- 126Magdaléna126

- Příspěvky: 30
- Reputace: 0
Re: určitý integrál per partes
↑ Freedy:
Ďakujem ti ;)
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » určitý integrál per partes (TOTO TÉMA JE VYŘEŠENÉ)

![kopírovat do textarea $\int_{a}^{b}\mathrm{e}^{x}\text{dx}=[\mathrm{e}^{x}]_a^b$](/mathtex/e0/e02734f1ff240ca5ee4c692378d356ea.gif)