Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 04. 05. 2009 19:08
#4 06. 05. 2009 17:47 — Editoval Marian (07. 05. 2009 15:55)
Re: Dělitelnost 10
Myslím, že jsem šel na úlohu jinak. Převáděl jsem uvedený typ sumy na geometrickou sumu modulo 5. Ukážu svůj postup pro řešení druhé úlohy. První úloha je snadná a jedná o speciální případ obecného, který uvedu.
Offline
#5 07. 05. 2009 15:48 — Editoval Pavel (07. 05. 2009 15:48)
Re: Dělitelnost 10
↑ Marian:
Drobně bych Tě Mariane poopravil:
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#6 07. 05. 2009 15:52 — Editoval Marian (07. 05. 2009 15:56)
Re: Dělitelnost 10
↑ Pavel:
Ano, už to vidím - unikla mi tahle skutečnost. Nicméně situace se nemění a postup je s diskuzí analogický. Znova by se ukázalo, že menší číslo než 43 nenajdeme. Podle Pavlovy připomínky jsem "drobně" poopravil svůj příspěvek s řešením.
Offline
#7 27. 06. 2010 21:12 — Editoval check_drummer (02. 07. 2010 17:35)
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Re: Dělitelnost 10
↑ Kondr:
Prohlížím si toto velmi staré téma a řešení mi není jasné. Pokud bude chuť se k němu vracet, měl bych otázku:
Děkuji za odpověď.
"Máte úhel beta." "No to nemám."
Offline
#8 17. 08. 2010 18:44
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Dělitelnost 10
↑ check_drummer: Důkaz je psaný dost zkráceně. Dojde se k tomu, že pro číslo tvaru k+20t (0<k<21) dává suma zbytek S(k)+4t po dělení 5, což je 0 právě pro t=5u+S(k). Z hlediska dělitelnosti 5 vyhoví právě čísla k+20(5u+S(k))=100u+k+20S(k) pro libovolné u, k. Kvůli dělitelnosti 2 je třeba některé hodnoty k vyloučit. Je to jasnější?
BRKOS - matematický korespondenční seminář pro střední školy
Offline

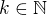 takové, že
takové, že
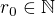 takové, že platí
takové, že platí
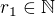 , že lze psát
, že lze psát 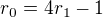 nebo
nebo 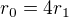 . V opačném případě nebude uvedená suma dělitelná dvojkou (důkaz sporem je jasný).
. V opačném případě nebude uvedená suma dělitelná dvojkou (důkaz sporem je jasný).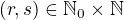 takových, že platí
takových, že platí 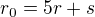 , kde
, kde  . Bude (mod 5)
. Bude (mod 5)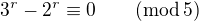 . Snadno se to dokáže indukcí. Odtud také máme důsledek pro lichá přirozená čísla r, totiž
. Snadno se to dokáže indukcí. Odtud také máme důsledek pro lichá přirozená čísla r, totiž  . Lze dokázat snadno indukcí, nebo se využije faktu
. Lze dokázat snadno indukcí, nebo se využije faktu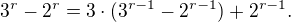
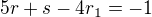 , která snadno plyne z toho, že
, která snadno plyne z toho, že  , tj.
, tj. 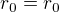 .
. . Odtud pro s=1 je
. Odtud pro s=1 je

 .
. 
 . Podobnou úvahou jako v bodě (3) dostaneme pro s=0 nejmenší možnou hodnotu r=13>8 (tak aby platilo P(r,s,r_1)). Podobně pro s=2 a s=4. Stačí vždy testovat maximálně do r=8. Ukáže se, že menší hodnotu pro číslo r již nelze dostat (tak aby platilo P(r,s,r_1) a suma byla kongruentní nula (mod 5)).
. Podobnou úvahou jako v bodě (3) dostaneme pro s=0 nejmenší možnou hodnotu r=13>8 (tak aby platilo P(r,s,r_1)). Podobně pro s=2 a s=4. Stačí vždy testovat maximálně do r=8. Ukáže se, že menší hodnotu pro číslo r již nelze dostat (tak aby platilo P(r,s,r_1) a suma byla kongruentní nula (mod 5)). 
 , nebo
, nebo 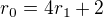 . Není však pravda, že v těchto případech nebude uvedená suma dělitelná dvojkou - co když
. Není však pravda, že v těchto případech nebude uvedená suma dělitelná dvojkou - co když