Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 17. 05. 2015 13:03 — Editoval Zlatohlavok (17. 05. 2015 13:06)
- Zlatohlavok
- Příspěvky: 312
- Reputace: 0
Určitý integrál
Ahojte, mám priklad s určitým integrálom, sú tu zadané podmienky.
Malo by sa to počítať zrejme tak, ak tomu správne chápem, že si zintegrujem 3 a následne 3x^2.
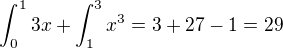
Mám to správne?
Ďakujem
Offline
- (téma jako vyřešené označil(a) Zlatohlavok)
#2 17. 05. 2015 13:54 — Editoval Freedy (17. 05. 2015 13:55)
Re: Určitý integrál
Ahoj,
ano, nicméně zápis je špatný.
Ty vlastně počítáš![kopírovat do textarea $\int_{0}^{1}3\text{dx}=[3x]^1_0=3 - 0 = 3$](/mathtex/8b/8be940af3444b0a9ad838c8f6bb6d721.gif)
![kopírovat do textarea $\int_{0}^{1}3x^2\text{dx}=[x^3]^3_1=27 - 1 = 26$](/mathtex/b5/b59f31589d8acc0254c19d380a93ecb8.gif)
Výsledek je v pořádku
Mám také dotaz pro ostatní, pokud se na to podívají
Nemělo by se náhodou u toho prvního integrálu psát:![kopírovat do textarea $\lim_{B\to1}\int_{0}^{B}3\text{dx}=\lim_{B\to1}[3x]^B_0=3$](/mathtex/20/204b3e0ba988831237f3d75b5c1e0508.gif) ? když je vlastně
? když je vlastně  ?
?
Nebo se tam uvádí limita pouze když je daný bod nedefinovaný / nevlastní?
U určitých integrálů jsem totiž vždy předpokládal uzavřenost intervalu.
Děkuji za odpověď
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
