Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 29. 05. 2015 12:28 — Editoval Bati (29. 05. 2015 12:31)
Re: Pocitani modulo
Ahoj,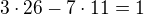 , takže
, takže
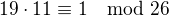 .
.
Pokud chceš mechanickej postup, jak spočítat inverz, hledej Euklidův algoritmus.
http://en.wikipedia.org/wiki/Extended_E … _algorithm
Offline
#6 29. 05. 2015 15:27 — Editoval Bati (29. 05. 2015 15:32)
Re: Pocitani modulo
↑ Mythic:
Když počítáš inverzi k 11 při mod 26, tak potřebuješ najít 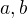 tak, aby
tak, aby 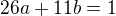 . Já jsem správná
. Já jsem správná 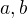 uhodl, protože jde o malá čísla. Pokud bys chtěl obecný návod, jak se ty čísla hledají, projdi si ten odkaz.
uhodl, protože jde o malá čísla. Pokud bys chtěl obecný návod, jak se ty čísla hledají, projdi si ten odkaz.
Na  není dobrý se dívat jako na desetinný číslo. Nevím, co umíš z algebry, ale je známo, že množina
není dobrý se dívat jako na desetinný číslo. Nevím, co umíš z algebry, ale je známo, že množina 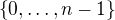 tvoří spolu s operacemi
tvoří spolu s operacemi 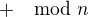 ,
, 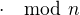 těleso. To mimo jiné znamená, že ke každému nenulovému prvku z množiny najdeš inverzní zase v té množině, takže nepotřebujeme zavádět žádná jiná čísla.
těleso. To mimo jiné znamená, že ke každému nenulovému prvku z množiny najdeš inverzní zase v té množině, takže nepotřebujeme zavádět žádná jiná čísla.
Edit: Je to těleso, pokud n je prvočíslo, což zde není, nicméně inverz k 11 stále existuje.
Offline
#8 29. 05. 2015 18:49
Re: Pocitani modulo
Poznamka
Vypocet ti uz ukazal ↑ Bati: tu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
