Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Didaktika a pedagogika: metodiky výuky a výukové materiály
- » Lineární ne/rovnice s absolutní hodnotou řešené úsudkem
#1 08. 07. 2015 21:00
- suprémum123

- Zelenáč
- Příspěvky: 4
- Reputace: 0
Lineární ne/rovnice s absolutní hodnotou řešené úsudkem
Dobrý večer,
mám zadání úloh:
Lineární rovnici a nerovnici s absolutní hodnotou řešte úsudkem /nikoli metodou nulových bodů/. 

Mohu poprosit o postup tak, aby byl didakticky správně?
Děkuji.
Offline
#2 08. 07. 2015 21:18
Re: Lineární ne/rovnice s absolutní hodnotou řešené úsudkem
↑ suprémum123:
Dobrý večer.
Zkuste využít toho, že absolutní hodnota čísla je vždy nezáporná.
What does a drowning number theorist say?
'log log log log ...'
Offline
#3 08. 07. 2015 22:20 — Editoval suprémum123 (08. 07. 2015 22:30)
- suprémum123

- Zelenáč
- Příspěvky: 4
- Reputace: 0
Re: Lineární ne/rovnice s absolutní hodnotou řešené úsudkem
↑ Andrejka3:
Samozřejmě z definice vycházím, tedy zde řešení jsou nasnadě.
Šlo mi spíš o "obecný postup", kdy rozpoznat, že se dá ne/rovnice vyřešit zmiňovaným úsudkem.
Lze tímto způsobem vyřešit např. obdobnou nerovnici pouze s tím, že změním součet na rozdíl?
Zadání by pak bylo:
Děkuji.
Offline
#4 08. 07. 2015 23:46
Re: Lineární ne/rovnice s absolutní hodnotou řešené úsudkem
↑ suprémum123:
Není mi jasné, co znamená 'řešit úvahou'.
Ke konkrétnímu příkladu:
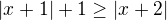 čtu asi takhle: x je od -2 vzdálené o jedna více než od -1 (rovnost) nebo míň (ostrá nerovnost).
čtu asi takhle: x je od -2 vzdálené o jedna více než od -1 (rovnost) nebo míň (ostrá nerovnost).
Takže kdyby x bylo vzdálené od -2 a -1 stejně, jsem v -1.5. Má být dál od -2 o jedna, proto se posunu doprava o 0.5. A jsem v -1. Teď je jasné, že když se posunu více doprava, vzdálím se o stejnou vzdálenost od obou bodů (-2 i -1), takže od -1 až nekonečno splňují rovnost.
Uvážím tu nerovnost -- mohu být i nalevo od -1. Řešením je celé R.
Takže Vás spíše zajímá, kdy použít kterou metodu k řešení. To nevím. Snad se ozvou další.
What does a drowning number theorist say?
'log log log log ...'
Offline
#5 09. 07. 2015 12:56 — Editoval Eratosthenes (09. 07. 2015 12:57)
- Eratosthenes
- Příspěvky: 2764
- Reputace: 136
Re: Lineární ne/rovnice s absolutní hodnotou řešené úsudkem
ahoj ↑ suprémum123:
nemám rád zadání typu "řešte úsudkem", protože nikde není pořádně napsáno, co to vlastně úsudek je, natož to, jaký úsudek je "didakticky správně". Podle definice MU "úsudek je schopnost řešit úvahou jednoduché problémy.... Obecný tvar úsudku je tento: P1,P2,...,Z" (viz http://www.muni.cz/tsp/usudky) což jsem pochopil jako množinu předpokladů, ze které odvodíš závěr. Jenže takto vypadá každá matematická úloha. Takže v tomto případě můžu z předpokladů (zadané nerovnice) usoudit, že nulové body jsou takové a makové z nich usoudit, že řešení vypadá takto. Takže i nulové body jsou "řešení úsudkem". Anebo si můžu vzpomenout, jak vypadají grafy funkcí 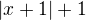 (modrý)
(modrý)  (zelený)
(zelený) 
a na základě znaménka >= usoudit, že modrý graf nesmí být níž než zelený. Takže i grafické řešení je "řešení úsudkem". Upřímně si nedovedu představit řešení, ke kterému by nějaký ten úsudek potřeba nebyl. Snad jenom něco bezmyšlenkovitě střelit, a pak jen doufat, že je to dobře. To ale zase není to, co si představujeme pod pojmem "řešení úlohy"...
Budoucnost patří aluminiu.
Offline
#6 09. 07. 2015 14:07
Re: Lineární ne/rovnice s absolutní hodnotou řešené úsudkem
↑ Eratosthenes:
S tím souhlasím. Ale s některými didaktiky je obtížné se přít. Zvlášť z pozice studenta.
What does a drowning number theorist say?
'log log log log ...'
Offline
#7 10. 07. 2015 17:06
- misaH
- Příspěvky: 13459
Re: Lineární ne/rovnice s absolutní hodnotou řešené úsudkem
:-)
Povedala by som, že pod "úsudkom" sa myslí riešenie použiteľné v pôvodných úlohách zadávateľa, kde je proste z vlastností (tuná ľavej strany) a hodnoty pravej strany riešenie takzvane jasné - tak štandardné postupy cez grafy ako aj cez odstraňovanie AH sú nadbytočné.
Zo základných vlastností usúdim na hodnotu výsledku bez ďalšieho použitia možných matematických postupov...
Offline
#8 11. 07. 2015 18:47
- check_drummer

- Příspěvky: 4896
- Reputace: 105
Re: Lineární ne/rovnice s absolutní hodnotou řešené úsudkem
Ahoj,  by bylo možné řešit tak, že jde vlastně o elipsu s ohnisky v bodech [a,0], [b,0] a délkou hlavní poloosy c/2. A elipsa má zřejmě střed v bodě (a+b)/2.
by bylo možné řešit tak, že jde vlastně o elipsu s ohnisky v bodech [a,0], [b,0] a délkou hlavní poloosy c/2. A elipsa má zřejmě střed v bodě (a+b)/2.
"Máte úhel beta." "No to nemám."
Offline
Stránky: 1
- Hlavní strana
- » Didaktika a pedagogika: metodiky výuky a výukové materiály
- » Lineární ne/rovnice s absolutní hodnotou řešené úsudkem