Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Odmocnina z komplexního čísla (TOTO TÉMA JE VYŘEŠENÉ)
#2 26. 09. 2015 16:14 — Editoval Freedy (26. 09. 2015 16:15)
Re: Odmocnina z komplexního čísla
Ahoj,
umocnit, vynásobit celou rovnici jmenovatelem (z se nerovná -2) a poté řešit kvadratickou rovnici přes vzorec, popřípadě jinou metodou.
nebo zavést substituci  vypočítat
vypočítat  a poté se vrátit k původní proměnné.
a poté se vrátit k původní proměnné.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#6 26. 09. 2015 17:13 — Editoval Freedy (26. 09. 2015 17:15)
Re: Odmocnina z komplexního čísla
Máš jen trošku špatné značení.  tedy
tedy >>>
>>>
Máš tedy dva kořeny
Pro k = 0
Pro k = 1
Sám si můžeš ověřit, že po umocnění těchto čísel, dostaneš původní hledanou odmocninu a tedy 2i

Nyní navrácení k původní rovnici.
Řešíš to jako 2 části. Pro  je to tedy:
je to tedy: vynásobíš celou rovnici (z+2)
vynásobíš celou rovnici (z+2) upravíš
upravíš
 nyní už pouze vydělíš celou rovnici ičkem a máš:
nyní už pouze vydělíš celou rovnici ičkem a máš: nicméně, takovýto tvar není konečný, musíš číslo převést do tvaru, kdy jsou patrné jeho obě složky. Usměrnit tedy zlomek tak, aby nebylo "i" ve jmenovateli. Tedy:
nicméně, takovýto tvar není konečný, musíš číslo převést do tvaru, kdy jsou patrné jeho obě složky. Usměrnit tedy zlomek tak, aby nebylo "i" ve jmenovateli. Tedy:
Druhá část je naprosto stejná
Na závěr provedeš zkoušku a ověříš správnost řešení:


L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Odmocnina z komplexního čísla (TOTO TÉMA JE VYŘEŠENÉ)





![kopírovat do textarea $|a|=\sqrt[n]{|z_{0}|}=\sqrt{2}$](/mathtex/27/273661d9cda5b9bd6efb2933079c5978.gif)

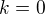






 vzdy.
vzdy. pro případ, kdy
pro případ, kdy