Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 28. 10. 2015 17:39 — Editoval xstudentíkx (28. 10. 2015 17:45)
- xstudentíkx


- Příspěvky: 962
- Škola: VŠE
- Pozice: student
- Reputace: 26
Vektorový prostor
Ahoj,
řeším jeden důkaz a zasekla jsem při dokazování neutrálního prvku. Prosím tedy někoho o radu.
Uvažujme množinu kladných reálných čísel 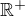 s operacemi
s operacemi 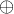 a
a 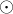
definovanými takto:

Dokažte, že  tvoří vektorový prostor.
tvoří vektorový prostor.
Nevím jak dokázat třetí axiom 
o = nulový vektor.
 , což nesplňuje axiom. Je mi jasné, že pokud dám o=1, tak to splněné bude, jenže to už zase nebude nulový vektor...
, což nesplňuje axiom. Je mi jasné, že pokud dám o=1, tak to splněné bude, jenže to už zase nebude nulový vektor...
Offline
#2 28. 10. 2015 17:52 — Editoval misaH (28. 10. 2015 17:54)
- misaH
- Příspěvky: 13460
Re: Vektorový prostor
↑ xstudentíkx:
Hľadáš neutrálny prvok vzhľadom na sčítanie.
Musí teda platiť  . Nič viac ani menej. Ak ho nájdeš, je to on.
. Nič viac ani menej. Ak ho nájdeš, je to on.
Nuly s tým nič nemajú.
Offline
#3 28. 10. 2015 18:05 — Editoval xstudentíkx (28. 10. 2015 18:13)
- xstudentíkx


- Příspěvky: 962
- Škola: VŠE
- Pozice: student
- Reputace: 26
Re: Vektorový prostor
↑ misaH:
Takže to mám brát tak, že mám najít čistě neutrální prvek, vzhledem k tomu, že o je vektor, se bude jednat o 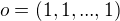 ?
?
Offline
#4 28. 10. 2015 18:21
- Eratosthenes
- Příspěvky: 2937
- Reputace: 139
Re: Vektorový prostor
ahoj, ↑ xstudentíkx:
>> Nulový vektor o je zvláštním případem vektoru...
to ano,
>> který lze zapsat jako uspořádanou n-tici 
to je bohužel špatně, protože to neplatí vždy - zrovna v našem případě ne (jednak nula není kladná, takže do našeho prostoru vůbec nepatří) a jednak - vektor v tomto případě není n-tice čísel, ale číslo jedno jediné. Rozhodující je, jak je nulový vektor definován, tj. pro každé u je 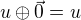 . V našem případě je tedy
. V našem případě je tedy 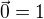
>> Norma nulového vektoru je rovna nule.
To není (tak docela) pravda. Ve vektorovém prostoru nemusí být norma vůbec definována (viz náš případ). Zde ani jeden vektor žádnou normu nemá.
Budoucnost patří aluminiu.
Offline
#5 28. 10. 2015 18:32
- xstudentíkx


- Příspěvky: 962
- Škola: VŠE
- Pozice: student
- Reputace: 26
Re: Vektorový prostor
↑ Eratosthenes:
Následně jsem si některé body uvědomila sama a příspěvek editovala. Rozhodně děkuji za objasnění, tedy definice z wikipedie není všeobecně správná. Ještě přesně nerozumím tomu, proč je v tomto případě vektor jen jedno jediné číslo?
Offline
#6 28. 10. 2015 18:57 — Editoval misaH (28. 10. 2015 18:58)
- misaH
- Příspěvky: 13460
Re: Vektorový prostor
Lebo jeho prvky sú reálne čísla (R+), máš to v definícii.
Offline
#7 28. 10. 2015 19:35
- xstudentíkx


- Příspěvky: 962
- Škola: VŠE
- Pozice: student
- Reputace: 26
Re: Vektorový prostor
↑ misaH:
Jo takto :) Děkuji už je mi to jasné
Offline