Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 21. 11. 2015 22:33 — Editoval Monograptus (21. 11. 2015 23:23)
- Monograptus

- Zelenáč
- Příspěvky: 22
- Škola: VŠST Liberec (SF, 78-83 Ing.)
- Reputace: 0
zajímavá vlastnost prvočísel
Narazil jsem na to v učebnici pro základní školy, je tam popsaná jedna vlastnost prvočísel, kterou dost nechápu.
výraz 
kde p je libovolné prčovíslo větší jak 3,
je bezezbytku dělitený dvanácti.
Proč?
Myslel jsem na malou větu Fermatovu, ale ta je o něčem jiném.
Offline
#2 21. 11. 2015 22:48 — Editoval misaH (21. 11. 2015 22:48)
- misaH
- Příspěvky: 13460
Re: zajímavá vlastnost prvočísel
↑ Monograptus:
Ahoj. :-)
prčovíslo
základná škola
Podivnosti...
Offline
#3 21. 11. 2015 23:16 — Editoval Monograptus (21. 11. 2015 23:21)
- Monograptus

- Zelenáč
- Příspěvky: 22
- Škola: VŠST Liberec (SF, 78-83 Ing.)
- Reputace: 0
Re: zajímavá vlastnost prvočísel
↑ misaH:
Jo, základní škola. Je to v kapitole o krácení zlomků. Rozkladem čitatele a jmenovatele na prvočísla a pak pokrácení.
Je to tahle knížka:
http://www.martinus.cz/?uItem=35986
Offline
#4 22. 11. 2015 09:13 — Editoval Honzc (22. 11. 2015 09:18)
Re: zajímavá vlastnost prvočísel
↑ Monograptus:
Zkusím ti to vysvětlit.
Výraz  si přepíšeme na tvar
si přepíšeme na tvar 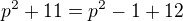
Protože číslo 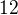 je jistě dělitelné
je jistě dělitelné 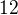 stačí dokázat, že
stačí dokázat, že  je dělitelné
je dělitelné 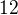 (pro
(pro  )
)
Nevím, jestli jste už brali vzoreček,  - jestli ne, tak věř, že je pravdivý.
- jestli ne, tak věř, že je pravdivý.
Potom 
Aby nějaké číslo bylo dělitelné 12 musí být dělitelné 3 a zároveň 4.
Protože každé prvočíslo větší než 3 je liché číslo musí být čísla 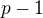 i
i 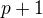 čísla sudá, a tedy každé z nich dělitelné 2. (pak tedy
čísla sudá, a tedy každé z nich dělitelné 2. (pak tedy  musí být dělitelné 4)
musí být dělitelné 4)
A teď ještě dokážeme, že  je dělitelné číslem 3.
je dělitelné číslem 3.
Vyslovíme tvrzení, že v každé trojici po sobě jdoucích čísel je právě jedno dělitelné 3. (to je asi zřejmé, že to tak je)
My máme takovou trojici: 
Protože číslo  je prvočíslo, nemůže být dělitelné 3 (pak by to nebylo prvočíslo)
je prvočíslo, nemůže být dělitelné 3 (pak by to nebylo prvočíslo)
A tedy jedno z čísel 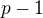 nebo
nebo 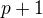 musí být dělitelné 3.
musí být dělitelné 3.
Tím jsme dokázali, že  je dělitelné
je dělitelné  a zároveň i
a zároveň i  , to znamená, že je dělitelné i
, to znamená, že je dělitelné i 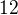
Potom i  je dělitelné
je dělitelné 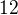 pro
pro 
Offline
#5 22. 11. 2015 09:23
- Akojeto
- Příspěvky: 465
Re: zajímavá vlastnost prvočísel
↑ Monograptus:
:-D
Len pre poriadok: učebnica to nie je. Sú to knižky pre záujemcov o matematiku (ktoré napísal tento pán). Sú zaujímavé a zábavné, ale priamo učebnice to nie sú. A pre základnú školu už vôbec nie.
Ale samozrejme, učebnica v zmysle "kniha z ktorej sa niekto učí" to pre niekoho byť môže.
Offline
#6 22. 11. 2015 10:11 — Editoval Monograptus (22. 11. 2015 10:15)
- Monograptus

- Zelenáč
- Příspěvky: 22
- Škola: VŠST Liberec (SF, 78-83 Ing.)
- Reputace: 0
Re: zajímavá vlastnost prvočísel
↑ Akojeto:
Aha, Já to koupil pro dítě v 4. tř. ZŠ.
Zlomky a průměr mi nosil jako domácí úkoly.
Offline
#7 22. 11. 2015 10:24
- Monograptus

- Zelenáč
- Příspěvky: 22
- Škola: VŠST Liberec (SF, 78-83 Ing.)
- Reputace: 0
Re: zajímavá vlastnost prvočísel
↑ Honzc:
Ó děkuji. Jak prosté.
Já v tom hledal bůhvíjaké složitosti.
Offline
#8 22. 11. 2015 11:02
Re: zajímavá vlastnost prvočísel
↑ Monograptus:
Ona se dá použít i ta Malá Fermatova věta, přímo z ní máme, že pro  máme
máme 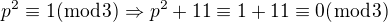 . A dále pro každé liché prvočíslo je
. A dále pro každé liché prvočíslo je 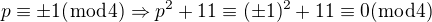 a jsme hotovi.
a jsme hotovi.
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#9 22. 11. 2015 11:15
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: zajímavá vlastnost prvočísel
Zdravím,
↑ Honzc: děkuji, neuměla jsem najít důkaz dělitelnosti 3 (začátek stejně).
↑ Monograptus: u nás v knihovně je tato série na dětském oddělení, jednu dobu jsem milému synovi (teď má 15) na přání půjčovala (ale hlavně dějepis) + doma máme "Děsivé míry a váhy", před časem přečetl a informace používal :-) Tedy pokud synovi vyhovuji styl, tak jako doplňková literatura určitě dobře.
Pro zajímavost uvedu další zdroje synova studia:
dějepis,
všechno možné a také všechno možné.
Naopak, když jsem ho nabádala, aby prošel testy, tak reagoval, zda nebude lepší, když si propočte sbírku. Tož si vyberte :-)
Offline