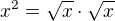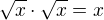Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 29. 12. 2015 16:37
Limity
Dobrý den,
Vůbec si nevím rady s jednou limitou, respektive si nejsem úplně jistý, co mi wolfram vyhodil.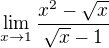 ...Zkoušel jsem rozšiřovat jak jmenovatelem, tak čitatelem, ale vždy z toho vyleze taková hnusnárna.
...Zkoušel jsem rozšiřovat jak jmenovatelem, tak čitatelem, ale vždy z toho vyleze taková hnusnárna.
Wolfram to řešil na dva kroky, které bohužel moc nechápu, sedím tady v tom už celý den.
Prosím o radu, děkuji :)
Offline
- (téma jako vyřešené označil(a) Tanner)
#8 29. 12. 2015 17:23
Re: Limity
jsem si rikal, ze si osvezim mozek po svatcich po dlouhe dobe tu na foru a takhle to dopada :D
druhy pokus:
zkus vydelit citatele vyrazem v jmenovali, jde to delit beze zbytku, pokud jsem nekde neudelal nejakou kravinu
Vykonávat věc, které se bojíme, je první krok k úspěchu.
Offline
#10 29. 12. 2015 17:39 — Editoval Al1 (29. 12. 2015 17:44)
Re: Limity
↑ Tanner:
Zdravím,
úprava čitatele : nejprve vytknutí 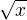 a pak rozklad na součin užitím vztahu
a pak rozklad na součin užitím vztahu 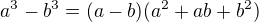
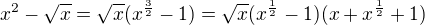
Je možné užít i L´Hospitalovo pravidlo.
Nejsem si jistý tvou úpravou " vše jsem si dal na druhou". To není ekvivaletní úprava.
Offline
#14 29. 12. 2015 17:59 — Editoval Sergejevicz (29. 12. 2015 17:59)
- Sergejevicz


- Příspěvky: 581
- Škola: Mgr. mat. a fyz. modelování na MFF UK v r. 2014
- Pozice: výpočtář
- Reputace: 21
- Web
Re: Limity
A co udělat středoškolsky tohle?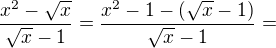
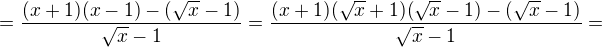
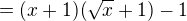
:-)
Kopáček: Mat. anal. nejen pro fyziky, Veselý: Zákl. mat. anal., Bečvář: Lin. alg., Matfyzpress
Bican: Lin. alg. a geom., Academia
Offline
#15 29. 12. 2015 18:05
- Sergejevicz


- Příspěvky: 581
- Škola: Mgr. mat. a fyz. modelování na MFF UK v r. 2014
- Pozice: výpočtář
- Reputace: 21
- Web
Re: Limity
Vlastn2 je to chztrá nula v čitateli - ve jmenovateli je výraz, který není v limitním bodě definován, tak co ho takhle vytvořit v čitateli, aby se pak zkrátil? V čitateli ho kus mám, mám tam tu odmocninu, tak přidám -1, musím ale hned zase vrátit, tím mi vznikne x^2 - 1, ze kterého by teď bylo vhodné taky vytknout tu odmocninu -1, tak použiju jednou a^2 - b^2 = (a+b)(a-b), to je3t2 nen9 ono, ale to (a-b) m8 vlastně tvar jako to s tou odmocninou, jen s druhou mocninou u každého členu, no tak tam použiju znova to co posledně a jsem doma, protože pak se tam objeví to s tou odmocninou, zkrátí se to, a pak už mám krásně všude, i v té jedničce (limitním bodě) definovaný a spojitý výraz, takže limita je pak funkční hodnota v jedničce.
Kopáček: Mat. anal. nejen pro fyziky, Veselý: Zákl. mat. anal., Bečvář: Lin. alg., Matfyzpress
Bican: Lin. alg. a geom., Academia
Offline
#16 29. 12. 2015 18:08
- Sergejevicz


- Příspěvky: 581
- Škola: Mgr. mat. a fyz. modelování na MFF UK v r. 2014
- Pozice: výpočtář
- Reputace: 21
- Web
Re: Limity
U substituce se vlastně používá věta o limitě složené funkce, takže tam se ještě má ověřit, že je splněna aspoň jedna ze dvou známých podmínek. Je splněna ta, že vnitřní funkce x = f(u) = u^2 nenabývá limitního bodu v okolí odpovídajícího argumentu.
Kopáček: Mat. anal. nejen pro fyziky, Veselý: Zákl. mat. anal., Bečvář: Lin. alg., Matfyzpress
Bican: Lin. alg. a geom., Academia
Offline