Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 10. 01. 2016 21:42 — Editoval Bati (10. 01. 2016 21:42)
Re: Neurčitý integrál
↑ malarad:
To samozřejmě můžeš, ale to nebyla má nápověda. Měl bys zjistit, že  . Zbytek integrálu, tj.
. Zbytek integrálu, tj.  můžeš spočíst z hlavy pomocí substituce.
můžeš spočíst z hlavy pomocí substituce.
Offline
#6 10. 01. 2016 22:03
Re: Neurčitý integrál
↑ malarad:
Chybí ti tam polovina v kosinu. Po úpravě dostaneš, co jsem napsal.
Offline
#7 10. 01. 2016 22:03
- van Thomas

- Příspěvky: 61
- Škola: FAV ZČU
- Reputace: 5
Re: Neurčitý integrál
Ahoj, i kdybys neznal (neuměl spočítat :)  , můžeš si napsat
, můžeš si napsat  . První je derivace
. První je derivace  , druhé jde spočítat z hlavy substitucí za
, druhé jde spočítat z hlavy substitucí za  :)
:)
Offline
#9 10. 01. 2016 22:18
- Sergejevicz


- Příspěvky: 581
- Škola: Mgr. mat. a fyz. modelování na MFF UK v r. 2014
- Pozice: výpočtář
- Reputace: 21
- Web
Re: Neurčitý integrál
Tohle je součástí obecného postupu, jak integrovat funkce s "proměnou" sin(x), cos(x). Substituce na t=tan(x/2) funkguje vždy. Užívá se tam trik, že se podívám na x v sinu a cosinu jako na dvojnásobný argument. Takže způsobem sin(x) = sin(2(x/2)), použiju vzorec pro sinus dvojnásobného argumentu, podobně por cosinus. Někde na to mám papír ze školy, najdu ho a třeba ho sem ofotím :-).
Kopáček: Mat. anal. nejen pro fyziky, Veselý: Zákl. mat. anal., Bečvář: Lin. alg., Matfyzpress
Bican: Lin. alg. a geom., Academia
Offline


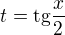 ?
?