Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 12. 01. 2016 20:35 — Editoval Freedy (12. 01. 2016 20:35)
Mohutnosti množin
Ahoj,
měl bych dvě otázky, které mi nejsou jasné ohledně mohutností množin.
Když mám větu  (kde P(X) je potenční množina X)
(kde P(X) je potenční množina X)
proč nelze větu dokázat tak, že ukážu, že existuje prosté zobrazení, které není na?
Například položím:
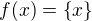
Každý prvek  tedy zobrazím na
tedy zobrazím na 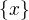 .
.
Žádné 2 prvky se tedy nezobrazí na stejný prvek - všechny prvky z X jsem použil.
Nicméně stále  tak, že tato množina nemá vzor.
tak, že tato množina nemá vzor.
Omlouvám se, jestli je to naprostá blbost, ale já zkrátka nechápu, proč toto nelze považovat za důkaz.
Další věc, která mi není jasná je to, proč, když existuje prosté zobrazení z A do B a zároveň existuje prosté zobrazení z B do A, pak tato zobrazení jsou zároveň na (intuitivně), se nepovažuje za důkaz Cantor-Bernsteinovy věty.
Díky,
Freedy
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#2 12. 01. 2016 21:23
Re: Mohutnosti množin
↑ Freedy:
k tomu prvnímu je problém v tom, že ta nerovnost která se tam správně dokazuje má být ostrá  . Tvým postupem dokážeš samozřejmě platnost neostré nerovnosti, ale pro ostrou to nestačí. Tam musíš dokázat, že neexistuje žádné prosté zobrazení NA. (příklad je množina přirozených a celých čísel, kde jako zobrazení použijješ identitu (je prostná, není NA, ale přesto mají stejnou mohutnost)).
. Tvým postupem dokážeš samozřejmě platnost neostré nerovnosti, ale pro ostrou to nestačí. Tam musíš dokázat, že neexistuje žádné prosté zobrazení NA. (příklad je množina přirozených a celých čísel, kde jako zobrazení použijješ identitu (je prostná, není NA, ale přesto mají stejnou mohutnost)).
U druhého problému ti (asi) vypadli nějaký slova, a takhle mi to nedává smysl. Ani nedokážu poznat na co jsi je chtěl zeptat.
Dva jsou tisíckrát jeden.
Offline
#3 13. 01. 2016 20:28
Re: Mohutnosti množin
Pozdravujem.
Poznamka.
V konecnom pripade tvoj dokaz ti umozni dokazat zaujimave veci.
Ale co myslis, ako by to funguvalo pre nekonecne nekonecne mnoziny?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 13. 01. 2016 20:48
Re: Mohutnosti množin
Ano, ta první věta se dokazuje tak, že předpokládáme, že existuje  , které je na.
, které je na.
Potom tedy ke každému 
 tak, že platí
tak, že platí  .
.
Uvažme množinu 
Tato množina je jistě prvkem P(X) protože se jedná podmnožinu X.
Musí tedy existovat  tak, že platí
tak, že platí 
Nyní může nastat jedna z následujících dvou situací:
1) tedy je
tedy je  ale
ale  čili
čili  spor
spor
2) tedy podle definice
tedy podle definice  čili
čili  spor.
spor.
↑ Wotton:
k té dvojce.
Hledal jsem způsob, jak nějak elegantněji dokázat Cantor-Bernsteinovu větu. Jak zkrátka ukázat, že pokud existuje prosté  a prosté
a prosté  pak f, g jsou zároveň na.
pak f, g jsou zároveň na.
↑ vanok:
tam je právě že problém s tou intuitivní představou no. Prostě vezmu dve prosté zobrazení
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline

 kde je prosté a na.
kde je prosté a na.