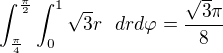Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Výpočet obsahu pomocí integrálů (TOTO TÉMA JE VYŘEŠENÉ)
#1 19. 01. 2016 19:47
- janca361

- .
- Příspěvky: 3284
Výpočet obsahu pomocí integrálů
Ahoj,
potřebuju spočítat následující:
Oblast mi tedy nepřijde zadaná jednoznačně, nicméně asi se má počítat červeá část (nebo ne?)
Počítala jsem tak, že jsem spočítala obsah dané výseče elipsy a od toho odečetla patřičnou výseč kruhu.
Integrály jsem sestavila následující:
Pro elipsu:
Pro kružnici:
Červené oblast mi vyšla: 
Výsledky integrálů mi podle WA sedí, kde je chyba? Mám ty integrály špatně sestavené nebo počítám na špatné oblasti?
Předem díky.
Offline
- (téma jako vyřešené označil(a) janca361)
#3 19. 01. 2016 21:03
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Výpočet obsahu pomocí integrálů
Zdravím,
mně se ještě nezdá převod rovnice elipsy a mezí pro elipsu do polárních souřadnic, jak jsi převáděla ↑ janca361:? OT: toto se podařilo? Děkuji.
Offline
#4 20. 01. 2016 12:28
#5 20. 01. 2016 13:41
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Výpočet obsahu pomocí integrálů
↑ janca361:
u transformace elipsy (pokud odvodíš ručně) dojdeš k výsledku, který se uvádí např. zde (od "in terms of polar coordinates..."), po úpravě na tvar 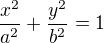 , potom Jakobian máš dobře, ale mez pro r je
, potom Jakobian máš dobře, ale mez pro r je  , úhel - souhlasím. Zkus buď ručně odvodit, nebo ještě projít např. příklad 1.2.7.
, úhel - souhlasím. Zkus buď ručně odvodit, nebo ještě projít např. příklad 1.2.7.
OT: to už bude Mauglí :-)
Offline
#6 20. 01. 2016 14:08 — Editoval Sergejevicz (21. 01. 2016 00:42)
- Sergejevicz


- Příspěvky: 581
- Škola: Mgr. mat. a fyz. modelování na MFF UK v r. 2014
- Pozice: výpočtář
- Reputace: 21
- Web
Re: Výpočet obsahu pomocí integrálů
↑ jelena:
↑ janca361:
Právě že pro elipsu chodí r od 0 do něčeho, co závisí na fí. Že to tak musí být, je vidět už z obrázku - pro každé fí (= natočení průvodiče) je bod na elipse jinak daleko od počátku (= pólu). Uvážil bych rovnici elipsy a vyjádřil bych z ní r. Horní mez pak bude 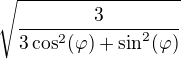 .
.
EDIT: Omluva, asi tam mám chybu. Níže opravím.
EDIT 2: Omluva 2. V tomto příspěvku se vyjadřuji k případu jiné transformace, viz níže http://forum.matweb.cz/viewtopic.ph … 00#p503000 .
Kopáček: Mat. anal. nejen pro fyziky, Veselý: Zákl. mat. anal., Bečvář: Lin. alg., Matfyzpress
Bican: Lin. alg. a geom., Academia
Offline
#8 20. 01. 2016 14:15
- janca361

- .
- Příspěvky: 3284
Re: Výpočet obsahu pomocí integrálů
↑ Sergejevicz:
Hm, jen jak ses k 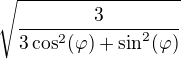 dostal?
dostal?
Offline
#9 20. 01. 2016 14:45
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Výpočet obsahu pomocí integrálů
↑ Sergejevicz:
děkuji, vím. 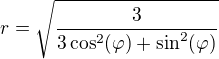 je odvození z původního zápisu elipsy. Pokud upravím na
je odvození z původního zápisu elipsy. Pokud upravím na 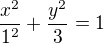 , potom při použití (např. viz odkaz poslední str.) dojdu k tomu, co jsem napsala. Souhlasíš?
, potom při použití (např. viz odkaz poslední str.) dojdu k tomu, co jsem napsala. Souhlasíš?
↑ janca361: on ten výsledek je nějaký zvláštní - proč by psali *4pi, když to jde vykrátit s jmenovatelem. Konec konců cca hodnotu výsledku můžeme odhadnout.
Offline
#10 20. 01. 2016 14:49 — Editoval Sergejevicz (21. 01. 2016 00:44)
- Sergejevicz


- Příspěvky: 581
- Škola: Mgr. mat. a fyz. modelování na MFF UK v r. 2014
- Pozice: výpočtář
- Reputace: 21
- Web
Re: Výpočet obsahu pomocí integrálů
↑ janca361:
Nebude. Zrovna jsem psal, jak vypadá horní mez integrálu.
↑ janca361:
Tak oprava je v podstatě v tom, zmíním dosazení přechodu od polárních souřadnic ke kartézským.
Jak jsem psal :-). "Uvážil bych rovnici elipsy a vyjádřil bych z ní r". Dobře - tak ne "uvážil bych", ale "uvažuju" :-).
Zapomněl jsem tam napsat, že se do rovnice elipsy dosadí přechod od polárních souřadnic ke kartézským.
(*)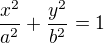
Transformace z polárních souřadnic do kartézských je
(**) ,
,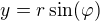 .
.
Dosadíme z (**) do (*), vyjádříme r a máme ,
,
což po dosazení za  ze zadání dává tu mez. :-)
ze zadání dává tu mez. :-)
Když jde o kružnici, je speciálen a = b = poloměr kružnice, a "r" by tak chodilo do (značme to) "a", což ze zadání je v případě kružnice 1.
EDIT: Omlouvám se, přehlédl jsem se, a tak se vlastně vyjadřuji k případu jiné transformace, viz níže http://forum.matweb.cz/viewtopic.ph … 00#p503000 .
Kopáček: Mat. anal. nejen pro fyziky, Veselý: Zákl. mat. anal., Bečvář: Lin. alg., Matfyzpress
Bican: Lin. alg. a geom., Academia
Offline
#11 20. 01. 2016 14:59
- Sergejevicz


- Příspěvky: 581
- Škola: Mgr. mat. a fyz. modelování na MFF UK v r. 2014
- Pozice: výpočtář
- Reputace: 21
- Web
Re: Výpočet obsahu pomocí integrálů
↑ jelena:
Moje myšlenka je spíš obráceně - mám útvar v kartézských souřadnicích, mám transformaci z jiných souřadnic do kartézských, tak dosadím, abych měl vše ve výrazech s těmi jinými souřadnicemi, a když mám štěstí, jako u elipsy nebo kružnice, dá se jedna ta nová souřadnice vyjádřit pomocí druhé.
Kopáček: Mat. anal. nejen pro fyziky, Veselý: Zákl. mat. anal., Bečvář: Lin. alg., Matfyzpress
Bican: Lin. alg. a geom., Academia
Offline
#12 20. 01. 2016 15:21 — Editoval janca361 (20. 01. 2016 15:32)
- janca361

- .
- Příspěvky: 3284
Re: Výpočet obsahu pomocí integrálů
↑ jelena:
On vyučující a autor řešení je taky trochu zvláštní, takže řešení vůbec nemusí být správně.
Mi třeba přijde zvlášní, že obsah je pro obě části stejný :)
↑ Sergejevicz:
Když to zkusím tvám způsobem, tak se dostanu k 
Zkoušela jsem úpravu 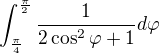 , ale ani to mi nějak nepomohlo k tomu, jak daný integrál spočítat.
, ale ani to mi nějak nepomohlo k tomu, jak daný integrál spočítat.
Trošku mi to sice připomíná vzorec 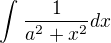 , ale pokus o substituci nikam nevede...
, ale pokus o substituci nikam nevede...
Offline
#13 20. 01. 2016 15:30
- Sergejevicz


- Příspěvky: 581
- Škola: Mgr. mat. a fyz. modelování na MFF UK v r. 2014
- Pozice: výpočtář
- Reputace: 21
- Web
Re: Výpočet obsahu pomocí integrálů
↑ janca361:
Chybí ti druhá mocnina u sin ve jmenovateli
To je standardní typ integrálu, viz
http://forum.matweb.cz/viewtopic.ph … 68#p502768
Kopáček: Mat. anal. nejen pro fyziky, Veselý: Zákl. mat. anal., Bečvář: Lin. alg., Matfyzpress
Bican: Lin. alg. a geom., Academia
Offline
#14 20. 01. 2016 15:55 — Editoval Sergejevicz (20. 01. 2016 15:55) Příspěvek uživatele Sergejevicz byl skryt uživatelem Sergejevicz. Důvod: Alternativní způsob výpočtu v kartézských souřadnicích. Na to někdy vytvořím nové téma. Zde skryto pro narušení běhu vlákna ve stylu polárních souřadnic.
#15 20. 01. 2016 16:36 — Editoval Jj (20. 01. 2016 16:37)
Re: Výpočet obsahu pomocí integrálů
↑ janca361:
Zdravím.
Řekl bych, že v polárních souřadnicích by měla jít uvedená ohraničená plocha spočítat takto: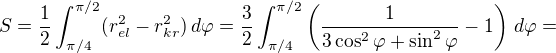
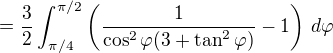
což by se mělo dát spočítat substitucí  ,
,
případně "druhá" označená plocha po změně mezí integrálu.
Pokud se tedy nemýlím.
Offline
#16 20. 01. 2016 16:40
- Sergejevicz


- Příspěvky: 581
- Škola: Mgr. mat. a fyz. modelování na MFF UK v r. 2014
- Pozice: výpočtář
- Reputace: 21
- Web
Re: Výpočet obsahu pomocí integrálů
↑ Jj:
Vždyť to jsme řešili tak, ale odděleně - zvlášť vnitřek elipsy a kruh a pak od sebe odečíst. :-)
Kopáček: Mat. anal. nejen pro fyziky, Veselý: Zákl. mat. anal., Bečvář: Lin. alg., Matfyzpress
Bican: Lin. alg. a geom., Academia
Offline
#17 20. 01. 2016 16:42 — Editoval Jj (20. 01. 2016 16:44)
Re: Výpočet obsahu pomocí integrálů
↑ Sergejevicz:
Tak pardon, těch příspěvku je už tolik, že jsem to ani moc neprohlížel, jen jsem neviděl nějaký konec :)
Pokud se tedy nemýlím.
Offline
#18 20. 01. 2016 23:26
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Výpočet obsahu pomocí integrálů
Zdravím v tématu,
já se ještě vrátím k postupu, který použila Janča:
Janča napsal(a):
já jsem napsal(a):
potom Jakobian máš dobře, ale mez pro r je
, úhel - souhlasím.
úhel nemám dobře, ještě musím použit přímku 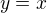 a tedy
a tedy  , odsud
, odsud  . Pro červenou část počítám
. Pro červenou část počítám  , pro zelenou část počítám
, pro zelenou část počítám  (v této variantě, mám dojem výsledek bude souhlasit s nabízeným).
(v této variantě, mám dojem výsledek bude souhlasit s nabízeným).
Akorát nejsem si jistá - nepracuji já teď s parametrickým vyjádřením (ne s polárním)? + skoro se to jeví, že bez použití dvojného integrálu (ale jen určitého) bychom se výsledků dostali spíš :-)
Offline
#19 21. 01. 2016 00:35 — Editoval Sergejevicz (21. 01. 2016 00:49)
- Sergejevicz


- Příspěvky: 581
- Škola: Mgr. mat. a fyz. modelování na MFF UK v r. 2014
- Pozice: výpočtář
- Reputace: 21
- Web
Re: Výpočet obsahu pomocí integrálů
↑ janca361:
Tobě a ostatním se omlouvám. Napsal jsem totiž, viz http://forum.matweb.cz/viewtopic.ph … 48#p502848 , že u elipsy chodí r do něčeho jiného než 1. A to je problém, protože postup Jancy361 používá transformaci šitou na míru elipse, totiž ,
,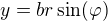 .
.
Tím se do Jacobiánu dostává ta 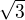 .
.
V takovém případě je horní mez pro r rovná 1, jak má i Jelena. Zjistí se to tak, jako jsem to dělal já, i když v jiném případě; dosadí se ty polárně-eliptické transformace do rovnice elipsy a vyjádří se r - v případě takovéto transformace je to skoro zadarmo. Je pak ale nutné správě určit úhel, jak se Jelena opravila tady:
http://forum.matweb.cz/viewtopic.ph … 95#p502995
Na druhé straně, já jsem uvažoval pro elipsu a její vnitřek transformace z obyčejných kruhových polárních souřadnic ,
,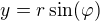 .
.
Tím mám Jacobián pouze obvyklé r. I dolní mez úhlu mi zůstane zřejmá z obrázku, právě díky kruhovosti transformace.
Ale horní mez r je složitější, jak jsem ukazoval tady:
http://forum.matweb.cz/viewtopic.ph … 66#p502866
Moje chyba spočívá v tom, že jsem nechal Jančin jakobián, ale k tomu dal svoji horní mez pro r.
Takže se ještě jednou omlouvám, chybu dám do příslušných editů, kterými se odkážu sem.
Až bude někdy čas, propočítám oba způsoby, a třeba i ten kartézský, ten viz skryté http://forum.matweb.cz/viewtopic.ph … 03#p502903 , musí to přeci vycházet stejně. :-)
Kopáček: Mat. anal. nejen pro fyziky, Veselý: Zákl. mat. anal., Bečvář: Lin. alg., Matfyzpress
Bican: Lin. alg. a geom., Academia
Offline
#20 21. 01. 2016 11:25
- janca361

- .
- Příspěvky: 3284
Re: Výpočet obsahu pomocí integrálů
↑ jelena: ↑ Sergejevicz:
Super, díky za vysvětlení.
Výsledek mám 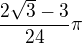 ,m což asi bude to, co bylo myšleno pod
,m což asi bude to, co bylo myšleno pod 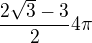 .
.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Výpočet obsahu pomocí integrálů (TOTO TÉMA JE VYŘEŠENÉ)
 . Počítal bych spíš tu oblast "z druhé strany přímky
. Počítal bych spíš tu oblast "z druhé strany přímky 
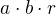 ,
, 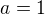 ,
,