Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Diferenciál.rovnice pomocí Laplaceovy transformace (TOTO TÉMA JE VYŘEŠENÉ)
#1 14. 02. 2016 19:47 — Editoval malarad (14. 02. 2016 19:49)
Diferenciál.rovnice pomocí Laplaceovy transformace
Ahoj, jak je možné, že z předmětu 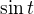 dostali obraz
dostali obraz  a ne
a ne 
pokud platí vztah mezi předmětem a obrazem 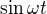 =
=  kde omega představuje číslo
kde omega představuje číslo
Ta dvojka na začátku v obrázku je jen číslo úlohy, není to součást zadání příkladu
Offline
- (téma jako vyřešené označil(a) malarad)
#2 14. 02. 2016 20:01 — Editoval Al1 (14. 02. 2016 20:03)
Re: Diferenciál.rovnice pomocí Laplaceovy transformace
↑ malarad:
Zdravím,
asi napsali chybně zadání. V daném materiálu řeší rovnici pro pravou stranu rovnu  . V závěru operují právě se vztahy pro sin(2t). Jinak ale pokud by rovnice byla zadaná
. V závěru operují právě se vztahy pro sin(2t). Jinak ale pokud by rovnice byla zadaná  , tak tomu odpovídá právě řešení z tvého materiálu.
, tak tomu odpovídá právě řešení z tvého materiálu.
Offline
#3 14. 02. 2016 20:24
Re: Diferenciál.rovnice pomocí Laplaceovy transformace
Ahoj ↑ malarad:,
Mas pravdu. Alebo ide o preklep ... Zial take sa casto stava.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Diferenciál.rovnice pomocí Laplaceovy transformace (TOTO TÉMA JE VYŘEŠENÉ)

