Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 … 9 10 11 12 13 … 25
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Limitny maraton
#251 13. 01. 2019 16:40
Re: Limitny maraton
Pozdravujem.
Problem(55)
Vysetrite rad vseobecneho clenu  ;
;  realne parameter.
realne parameter.
Mozme sa inspirovat aj navodom, ktory som dal v probleme (53).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#252 13. 01. 2019 19:11 — Editoval krakonoš (13. 01. 2019 19:28)
Re: Limitny maraton
↑ vanok:
Na jmenovatele použijeme vzorec pro rozdíl čtverců.
Dále roznásobíme závorky v čitateli a rozdělíme výraz na čtyři zlomky . Následně sloučíme první člen s posledním ve člen
. Následně sloučíme první člen s posledním ve člen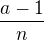 .
.
Dostaneme tak pro 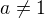 člen harmonické řady.Zbývající dva výrazy jsou členy konvergentních řad podle Leibnizova kriteria.Takže zadaná řada pro
člen harmonické řady.Zbývající dva výrazy jsou členy konvergentních řad podle Leibnizova kriteria.Takže zadaná řada pro 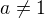 diverguje, a pro
diverguje, a pro 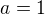 konverguje.
konverguje.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#253 13. 01. 2019 19:54
Re: Limitny maraton
Ahoj ↑ krakonoš:,
To je tiez mozne dobre riesenie.
Tiez sa daju pozuit vhodne rozvoje.
A aj mozme vyuzit, ze pre 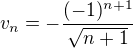 je
je
je konstantneho znamienka a ekvivalentna z 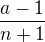 .
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#254 13. 01. 2019 21:49 — Editoval krakonoš (13. 01. 2019 21:52)
Re: Limitny maraton
↑ vanok:
Také dobré řešení.Ono vlastně stačí nahradit tu poslední závorku ve jmenovateli např 2,dostaneme divergentní řadu, která je menší než tato. Nebo vzít limitu té závorky t.j. 1, takže řada nemůže konvergovat, protože nekonverguje a-1/n+1 - podle Abelova kritéria
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#255 14. 01. 2019 17:30 — Editoval vanok (14. 01. 2019 17:31)
Re: Limitny maraton
Pripomeniem tento problem ( dal som ho uz davno na fore, no neviem nast kde je).
Problem(56*)
Vysetrite rad ktoreho vsebecny clen je 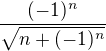 .
.
Je zaujimave sa nad nim zamysliet.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#256 14. 01. 2019 23:51
Re: Limitny maraton
Pripomenienka : problem 54 nie je este vyrieseny.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#257 15. 01. 2019 11:50
Re: Limitny maraton
↑ vanok:
Ahoj.
Tady by asi stačilo vytknout mínus a čitatele umocnit na n+1.Řadu rozepíšeme a dáme vždy do závorky dva členy-tak jak jdou po sobě.
Zároveň si rozepíšeme řadu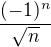 a uzávorkujeme po dvou členech.
a uzávorkujeme po dvou členech.
Součty v závorkách jsou u obou řad stejné.Zadaná řada by tedy měla konvergovat.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#258 15. 01. 2019 22:54 — Editoval vanok (15. 01. 2019 23:02)
Re: Limitny maraton
Ahoj ↑ krakonoš:,
Dobre, mozes podrobne napisat tvoju metodu pre foristov, co takto ucinne studuju.
Pripominam, ze som pouzil na toto cvicenie, ze  co zarucuje konvergenciu radu.
co zarucuje konvergenciu radu.
Mala doplnujuca uvaha.
Ako to je z radom vseobecneho clenu  , a realny parameter ?
, a realny parameter ?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#259 16. 01. 2019 00:34 — Editoval krakonoš (16. 01. 2019 01:08)
Re: Limitny maraton
↑ vanok:
Ahoj.
No,když to tak narychlo zkouším,připadá mi na první pohled,že pro a větší jak nula se daří dodržet pravidlo klesající funkce pro Leibnizovo kriterium (ten vytknutý člen).Pro a rovno nule to nedává vůbec smysl (dělení nulou)a v ostatních případech nebude limita zbytku rovna nule např pro a mínus jedna ta limita neexistuje a tak to bude asi i v dalších případech-kazí to tam to minus jedna na ntou pod odmocninou.
Měj se hezky.Musím dělat ještě spoustu jiných věcí.Poslední dobou se mi to nějak nakupilo!✋
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#260 16. 01. 2019 03:48 — Editoval vanok (16. 01. 2019 03:57)
Re: Limitny maraton
Pozdravujem ↑ krakonoš:,
Ked pouzijes metodu co som pouzil, mas okamzite :
Pre  rad konverguje a inac je divergentny.
rad konverguje a inac je divergentny.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#261 16. 01. 2019 03:56 — Editoval vanok (16. 01. 2019 03:57)
Re: Limitny maraton
Pozdravujem ↑↑ Bati:,
Tvoj problem(54) zatial nikoho neoslovil.
Moja myslienka je urobit ako prve Taylor-Young-ov rozvoj dostatocneho radu tvojej implicitnej fonkcie  .
.
Je to tak aj v tvojom rieseni.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#262 16. 01. 2019 16:03
Re: Limitny maraton
ahojte
vravím si že sa zapojím netradične, problém (54) som skúsil pomocou vety o implicitnej funkcii a l'Hospitalovho pravidla
funkcia  je nekonečne diferencovateľná
je nekonečne diferencovateľná
takže bude aj implicitná funkcia  taká že
taká že 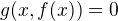 na vhodnom okolí bodu
na vhodnom okolí bodu 
predpoklady vety o implicitnej funkcii sú splnené takže bude  a zároveň je
a zároveň je 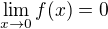
z derivácie rovnice 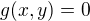 sa dostane
sa dostane 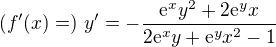 a teda aj
a teda aj 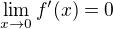
z derivácie rovnosti pre  sa dostane škaredý zlomok ako vyjadrenie pre
sa dostane škaredý zlomok ako vyjadrenie pre 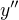 , ktorý pre
, ktorý pre 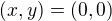 dáva
dáva 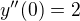
z toho všetkého je potom 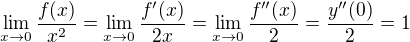 ak som niekde neurobil chybu
ak som niekde neurobil chybu
čo by ma zaujímalo je nejaké krajšie riešenie než toto drevorubačské
Offline
#263 16. 01. 2019 17:03
Re: Limitny maraton
↑ jardofpr:
Jestli existuje elegantnejsi reseni nevim, moje je stejne (priklad jsem tak konstruoval). Zaverecna cast se muze udelat nekolika zpusoby (L'Hospital, Taylor, aritmetika limit)
Offline
#264 18. 01. 2019 18:08 — Editoval vanok (18. 01. 2019 18:09)
Re: Limitny maraton
Pozdravujem,
Problem (57)
Vysetrite rad vseobecneho clenu  , kde
, kde  je realne cislo.
je realne cislo.
Aka je jeho suma pre 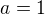 ?
?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#265 18. 01. 2019 18:41
#266 18. 01. 2019 20:01 — Editoval vanok (18. 01. 2019 20:27)
Re: Limitny maraton
Tu Servus ↑ laszky:,
Vyborne aj ked sa to da urobit o mnoho rychlejsie
Akurat na tu prvu otazku, by som pridal, ze: Ten rad konverguje pre kazde
 ( kazdy najde vhodny test na to).
( kazdy najde vhodny test na to). Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#267 18. 01. 2019 20:19
Re: Limitny maraton
Pozdravujem,
Hned pridavam dalsi
Problem (58)
Nech  je funkcia definovana na inrervalle
je funkcia definovana na inrervalle ![kopírovat do textarea $[-1;1]$](/mathtex/da/da2c2fdd674c02facae5273b4cb759a4.gif) taka, ze
taka, ze  a ze je dérivabilna v bode
a ze je dérivabilna v bode  . Nech
. Nech  , je prirodzene nenulove cislo, urcite
, je prirodzene nenulove cislo, urcite 
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#268 19. 01. 2019 17:19 — Editoval vanok (20. 01. 2019 08:41)
Re: Limitny maraton
Problem 58,
Hint 1.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#269 19. 01. 2019 19:15 — Editoval jardofpr (19. 01. 2019 19:17)
#270 24. 01. 2019 19:36
#272 24. 01. 2019 23:01
#273 24. 01. 2019 23:24
Re: Limitny maraton
↑ jardofpr:
Diky.Uz chapu jak to bylo mysleno.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#274 25. 01. 2019 13:19
#275 25. 01. 2019 13:26 — Editoval krakonoš (25. 01. 2019 13:29)
Re: Limitny maraton
↑ jardofpr:
Ahoj.
Zkoušela jsem si pro zajímavost ten případ kdy je x umocněno na xnaxtou.
Vyšla jsem z toho,že 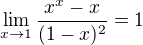 a s využitím této informace spočítat
a s využitím této informace spočítat 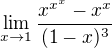 .Vyšla mi -1.Takže už zde vidím jistou stabilitu při porovnání s odpovídajícím polynomem (že by se mohly chovat stejně).Jedině se mi změnilo to znaménko, jestli jsem se nespletla ovšem.Takže zadaná limita by mohla být -1,pokud by docházelo k střídání znamének .
.Vyšla mi -1.Takže už zde vidím jistou stabilitu při porovnání s odpovídajícím polynomem (že by se mohly chovat stejně).Jedině se mi změnilo to znaménko, jestli jsem se nespletla ovšem.Takže zadaná limita by mohla být -1,pokud by docházelo k střídání znamének .
Koukám,že jsme se shodli jak časově tak na výsledku.To se mi ještě nestalo.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
Stránky: 1 … 9 10 11 12 13 … 25
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Limitny maraton

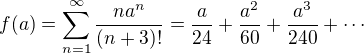 , potom
, potom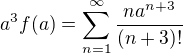 , a proto
, a proto  , neboli
, neboli  .
.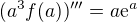 , a proto
, a proto  .
.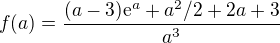 a
a  .
. a podobna rovnost aj vo vseobecnom pripade (co nebolo pytane v danom texte)
a podobna rovnost aj vo vseobecnom pripade (co nebolo pytane v danom texte) 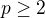 .
.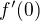 je limita pre
je limita pre 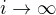 vyrazu
vyrazu  .
.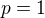 máme postupnosť
máme postupnosť  , zo spojitosti
, zo spojitosti 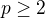
 môžme písať
môžme písať![kopírovat do textarea $f(x) = [f'(0)+\varphi (x)]x$](/mathtex/4b/4be6e23b1788877d15575789dcade08a.gif) pričom
pričom 

 -tý člen postupnosti:
-tý člen postupnosti: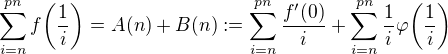
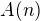 a
a 
 je
je ![kopírovat do textarea $A(n) = f'(0)(H_{pn}-H_{n-1}) = f'(0)\bigg[[H_{pn}-\ln{(pn)}]+\ln{\bigg(\frac{pn}{n-1}\bigg)}+[\ln{(n-1)}-H_{n-1}]\bigg]$](/mathtex/5d/5d0c47963a8ee8b8e7dba868a84e5b47.gif)
![kopírovat do textarea $\lim_{n\to\infty} A(n) = f'(0)[\gamma + \ln{(p)} -\gamma] = f'(0)\ln{(p)}$](/mathtex/36/369292ab97e27fc20769d4513cca9577.gif)

 tak, že pre
tak, že pre  je
je 
 existuje prirodzené
existuje prirodzené  tak, že
tak, že 
 je
je![kopírovat do textarea $|B(n)| = \bigg| \sum_{i=n}^{pn}\frac{1}{i}\varphi\bigg(\frac{1}{i}\bigg)\bigg|\leq \sum_{i=n}^{pn}\frac{1}{i}\bigg|\varphi\Big(\frac{1}{i}\Big)\bigg|\leq \frac{\varepsilon}{n}[pn-(n-1)]<\frac{\varepsilon}{n}pn=p\varepsilon$](/mathtex/52/5272a45a903fc2095574de02d101f224.gif)

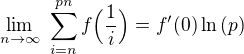
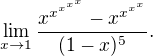


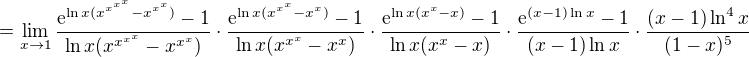
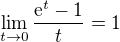 and equivalently
and equivalently