Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 27. 05. 2009 20:01 — Editoval Olin (27. 05. 2009 20:39)
Re: limita
Limita součtu je součet limit (pokud jsou obě vlastní), takže počítáme vlastně 2 limity.
Ta první: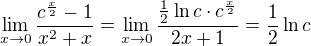
ovšem za podmínky  . Při výpočtu jsem použil l'Hospitalovo pravidlo. Pro ostatní c není limita definována.
. Při výpočtu jsem použil l'Hospitalovo pravidlo. Pro ostatní c není limita definována.
Druhá: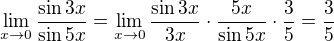
Je možné postupovat i přes l'Hospitalovo pravidlo, je to rychlejší.
Offline
#4 29. 05. 2009 20:23
Re: limita
lim (sqrt(x^3-1)-2)/ sqrt(x^2-1) jdoucí k minus nekonečnu, můžete mi, prosím, vysvětlit, proč lim x^(3/2) jdoucí k minus nekonečnu je nekonečno
Smutné je, že hlupáci jsou tak sebejistí, zatímco moudří lidé jsou vždy plní pochybností.“ — Bertrand Russell
Offline
#5 29. 05. 2009 20:43
Re: limita
↑ adjamot:
Víš určitě,že to je nekonečno? Mě se zdá, že to neni definovaný nebo že to je 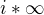
Do prázdného domu vešli 4 lidé, poté odešlo 6 lidí. Kolik lidí musí do domu vejít, aby byl dům prázdný?
Offline
#6 30. 05. 2009 12:20
Re: limita
↑ Asinkan: je to nekonečno, pokud je ve výrazu i*nekonečno i myšleno reálné číslo vyjde to opět nekonečno
Smutné je, že hlupáci jsou tak sebejistí, zatímco moudří lidé jsou vždy plní pochybností.“ — Bertrand Russell
Offline

 :-)
:-)