Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematických struktur
- » Vnořené podmnožiny spočetné množiny (TOTO TÉMA JE VYŘEŠENÉ)
#1 25. 04. 2016 17:17
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Vnořené podmnožiny spočetné množiny
Ahoj,
dokažte, že existuje lineárně uspořádaný (vzhledem k inkluzi) system F množin, které jsou podmnožinou spočetné množiny A, takový, že F je nespočetný. Tj. F obsahuje množiny takové, že všechny jsou částí A a pro libovolné X,Y z F je buď  nebo
nebo  a množin v F je nespočetně mnoho. Zní to skoro neuvěřitelně.
a množin v F je nespočetně mnoho. Zní to skoro neuvěřitelně.
"Máte úhel beta." "No to nemám."
Offline
- (téma jako vyřešené označil(a) check_drummer)
#2 27. 04. 2016 16:40
- Eratosthenes
- Příspěvky: 3110
- Reputace: 140
Re: Vnořené podmnožiny spočetné množiny
ahoj ↑ check_drummer:,
dokázat by měl umět každý student matematiky v prvním semestru. Věta je uvěřitelná nebo neuvěřitelná stejně, jako je uvěřitelná nebo neuvěřitelná existence množiny všech reálných čísel :-)
Budoucnost patří aluminiu.
Offline
#3 29. 04. 2016 17:48
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Vnořené podmnožiny spočetné množiny
Nápověda: Použijte jako spočetnou množinu množinu racionálních čísel.
"Máte úhel beta." "No to nemám."
Offline
#4 29. 04. 2016 17:49
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Vnořené podmnožiny spočetné množiny
↑ Eratosthenes:
Když ho napadne jak na to, je to velmi snadné. :-) Kolumbovo vejce...
"Máte úhel beta." "No to nemám."
Offline
#5 29. 04. 2016 17:51
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Vnořené podmnožiny spočetné množiny
↑ Eratosthenes:
No dalo by se to brát tak, že každá ta podmnožina "určuje" nějaké číslo, protože je "větší" než všechny množiny, které obsahuje - a tedy je podivné, že je spočetná, ale těch vnořených množin je nespočetně. Ale takto přímo uvažovat nelze - protože nelze vybrat číslo, které není obsaženo žádné množině v ní obsažených.
"Máte úhel beta." "No to nemám."
Offline
#6 30. 04. 2016 00:01 — Editoval Stýv (30. 04. 2016 08:19)
- Eratosthenes
- Příspěvky: 3110
- Reputace: 140
Re: Vnořené podmnožiny spočetné množiny
↑ check_drummer:
Takže asi prozradím.
Budoucnost patří aluminiu.
Offline
#7 01. 05. 2016 18:18
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Vnořené podmnožiny spočetné množiny
↑ Eratosthenes:
Ano, správně.
"Máte úhel beta." "No to nemám."
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematických struktur
- » Vnořené podmnožiny spočetné množiny (TOTO TÉMA JE VYŘEŠENÉ)
 a pro každé
a pro každé 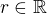 sestrojme množinu
sestrojme množinu  . Pro každé
. Pro každé  je zřejmě
je zřejmě  , takže systém všech množin
, takže systém všech množin 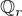 je lineárně uspořádaný inkluzí. A protože zobrazení
je lineárně uspořádaný inkluzí. A protože zobrazení  je zřejmě bijekce, je množina všech
je zřejmě bijekce, je množina všech