Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 13. 06. 2016 16:26
Je tohle dobře?
Dobrý den. Je tohle dobře, prosím? Přiznávám, že mám nějak vypnuto a nemůžu to rozlousknout. Díky.
Při pádu z malé výšky může dopadnout těžší a větší těleso dříve než těleso menší a lehčí, ale při pádu z větší výšky to může být naopak. Jelikož jsme si řekli, že odporová síla závisí na rychlosti, proto při pádu z malé výšky nemusí větší těleso nabrat velkou rychlost a tím nevzroste odporová síla natolik, aby tolik brzdila. Z větší výšky pak rychlost vzroste více, tím i odporová síla, a může tak ustálit těžší těleso na konečné nižší rychlosti než těleso lehčí.
Fyzika a matematika konečně srozumitelně - www.nabla.cz
Fyzikální bludy
Řešení státní maturity z matematiky
Kdy psát mě a mně
Offline
#2 13. 06. 2016 19:06
Re: Je tohle dobře?
↑ Peta8:
Hezký den,
to vůbec není jednoduchá úvaha, protože do řešení se promítne i to, jakou předpokládáš závislost odporové síly na rychlosti. Pokud se např. budete předpokládat, že odporová síla je přímo úměrná čtverci rychlosti s konstantou úměrnosti k, můžeš si sestavit diferenciální rovnici pro rychlost pádu tělesa o hmotnosti m(pokud jsem se nespletl):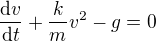
Tak od oka (no zase až tak od oka ne, ale spíše první nápad bez konktroly řešení - a já dělám početní chyby..) by mohla být řešením každá funkce ve tvaru: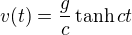
, kde c je kladná nenulová konstanta, ve které je ukryta hmotnost tělesa m a výše zmíněná konstanta úměrnosti k.
Dráhu lze vypočítat integrací, pokud se nemýlím, tak:
Tady by dalo mechanicky ověřit, že pro dvě různé c1 a c2 bude pro každé t>0 platit, že odpovídající s1(t) je různé od s2(t). To bych řekl, že platí (neověřeno). Tedy za předpokladu, že platí Newtonův odporový vzorec, je dotazované tvrzení nepravdivé.
Доктор сказал «в морг» — значит в морг!
Offline
