Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 24. 09. 2016 12:08
Charakteristika tělesa
Zdravím, mám za sebou první přednášku Lineární algebry a geometrie a jsem z toho celkem špatný.
Nějak jsem se skriptami přelouskal k charakteristice tělesa. Máme napsáno, že charakteristika tělesa je n*1=0, kdy "n" je nejmenší kladné celé číslo, které tuto rovnost splňuje a když takové "n" neexistuje, je charakteristika rovna nekonečnu. Nejde mi do hlavy, jak by mohla být charakteristika jiná než nekonečno, tj. jak může n*1 dát někdy nulu ?
Díky moc.
Offline
#2 24. 09. 2016 12:53
Re: Charakteristika tělesa
Ahoj,
Odpoved je ano.
Mysli napr. na teleso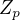 
prvkov modulo p, ( zvyskov celych cisiel po deleni p), kde p je prvocislo.
Vtedy jeho characteristika je p.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 24. 09. 2016 14:24 — Editoval misaH (24. 09. 2016 14:32)
- misaH
- Příspěvky: 13467
Re: Charakteristika tělesa
↑ holyduke:
:-)
Kondr:
Charakteristika je nejmenší takové x, pro které platí, že když sečteme x jedniček, dostaneme nulu. Pokud takové x neexistuje, říkáme, že je charakteristika tělesa nulová. Charakteristika je vždy nula nebo přirozené číslo.
(...)
Ale ak sa tá 0 vlastne rovná nekonečnu, tak potom dobre.
Offline
#8 24. 09. 2016 21:51 — Editoval misaH (24. 09. 2016 22:09)
- misaH
- Příspěvky: 13467
Re: Charakteristika tělesa
↑ Fonzik:
Vysvetlil ti to už vanok.
Ak tomu nerozumieš, pomoc je ťažká.
Daj si do Googlu slová "teleso modulo".
Zvyšky po delení nejakým číslom totiž tvoria konečnú množinu. A tam keď zratúvaš jednotky, nemôžeš prekročiť maximálnu hranicu - "podiel" by sa zvýšil a zvyšky sa opakujú - ako píše jarrro.
Pri delení piatimi sú zvyšky len 0,1,2,3,4 zvyšok 5 už nemôže byť. Keď 5krát sčítaš jednotku, dostaneš "znova" nulu ako keď ju sčítaš nulakrát. Zvyšok po delení piatich piatimi je totiž 0 a tu sa pracuje so zvyškami po delení.
Offline