Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 11. 10. 2016 12:07 — Editoval Vladislav97 (11. 10. 2016 12:07)
- Vladislav97

- Místo: Praha
- Příspěvky: 421
- Škola: Gymnázium
- Pozice: Student (Druhák)
- Reputace: 13
Vyjádření ze vzorce
Zdravím,
chci se zeptat na vyjádření neznáme  ze vzorce
ze vzorce 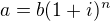 . Má to vyjádření mít nějakou hlubší myšlenku? Já jsem došel k tomuto:
. Má to vyjádření mít nějakou hlubší myšlenku? Já jsem došel k tomuto: ![kopírovat do textarea $\sqrt[n]{\frac{a}{b}}-1=i$](/mathtex/3c/3c0ed137f8fe3c6ecbcc70bf120697df.gif) . Ale nějak mi to nesedne...
. Ale nějak mi to nesedne...  může být buď sudé nebo liché. Pak záleží, jestli v jednom kroku pro sudá čísla nezapsat
může být buď sudé nebo liché. Pak záleží, jestli v jednom kroku pro sudá čísla nezapsat ![kopírovat do textarea $ \sqrt[n]{\frac{a}{b}}=|1+i|$](/mathtex/2a/2a1c02e9c10cef33e5156b1462261df5.gif) a pak to nějak dovyjádřit$. Příjde mi, že se to pak bude větvit do několika možností. Neřeší se to nějak přes binomický rozvoj?
a pak to nějak dovyjádřit$. Příjde mi, že se to pak bude větvit do několika možností. Neřeší se to nějak přes binomický rozvoj?
Předem díky.
Offline
#2 11. 10. 2016 12:34 — Editoval Rumburak (11. 10. 2016 13:45)
Re: Vyjádření ze vzorce
↑ Vladislav97:
Ahoj.
Binomický rozvoj zde nepomůže. Substitucí  bych danou rovnici zjednodušil na
bych danou rovnici zjednodušil na 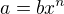 .
.
Jestliže 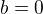 , pak je diskuse řešitelnosti velmi jednoduchá. V opačném případě vydělíme rovnici číslem
, pak je diskuse řešitelnosti velmi jednoduchá. V opačném případě vydělíme rovnici číslem 
a řešíme rovnici tvaru  ....
....
Offline