Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 21. 10. 2016 19:01 — Editoval dominiksep (21. 10. 2016 19:09)
- dominiksep
- Příspěvky: 54
- Reputace: 0
Příklad na vektorové prostory matic
Ahoj,
mám následující příklad na vektorové prostory matic a nemůžu s ním pohnout:
Mám zjistit, zda V je vektorový prostor při zúžení operací z prostoru matic 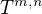 . Pokud ano, mám najít báze V a ověřit, že jde o báze V.
. Pokud ano, mám najít báze V a ověřit, že jde o báze V.
Co se týče dosavadního postupu, mám menší problém s pochopením definice vektorového prostoru matic - respektive pokud mám někde uvedeno "vektorový prostor matic 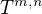 nad číselným tělesem T", znamená to, že všechny matice v daném prostoru mají stejnou velikost?
nad číselným tělesem T", znamená to, že všechny matice v daném prostoru mají stejnou velikost?
V dalším postupu jsem předpokládal, že matice jsou stejně velké. V tom případě snadno dokážu uzavřenost na sčítání a násobení číslem z tělesa. Problém ale nastává u nalezení vektorů báze. Původně jsem myslel, že bych mohl mít  vektorů báze, přičemž
vektorů báze, přičemž  z nich vynásobených vždy prvkem
z nich vynásobených vždy prvkem 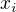 a s
a s  tým jedničkovým řádkem a
tým jedničkovým řádkem a  vektorů vynásobených vždy prvkem
vektorů vynásobených vždy prvkem 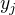 s
s 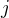 tým jedničkovým sloupcem.
tým jedničkovým sloupcem.
Takový systém vektorů báze by ovšem nebyl lineárně nezávislý (vždy jeden vektor by šel vyjádřit pomocí ostatních) a nemůžu si dovolit žádný z vektorů škrtnout.
Nemůžete mi prosím poradit, jakým směrem se vydat?
Děkuji,
Dominik
Offline
#2 21. 10. 2016 19:03 Příspěvek uživatele dominiksep byl skryt uživatelem dominiksep. Důvod: Není aktuální
#4 21. 10. 2016 19:30
- dominiksep
- Příspěvky: 54
- Reputace: 0
Re: Příklad na vektorové prostory matic
↑ Stýv:
No nevidím, protože pokud ho škrtnu, tak potom matice podle nových bází vyjádřená nebude mít vlastnosti ze zadání (jeden řádek/sloupec prostě nebude sedět).
Offline
#5 21. 10. 2016 19:50
- dominiksep
- Příspěvky: 54
- Reputace: 0
Re: Příklad na vektorové prostory matic
Pro ukázku jak to myslím uvádím příklad bází pro matici 3x3:

Ovšem například 1. matici lze vyjádřit jako -1*(druhá+třetí)+1*(čtrvrtá+pátá+šestá)
Offline
#6 21. 10. 2016 20:40
Re: Příklad na vektorové prostory matic
↑ dominiksep: ... takže se bez té první matice obejdeš
Offline
#7 21. 10. 2016 21:04
- dominiksep
- Příspěvky: 54
- Reputace: 0
Re: Příklad na vektorové prostory matic
↑ Stýv:
No ale m*n prvků nemůžu přece vyjádřit pomocí m*n-1 vektorů báze. Pokud se pokusím takto vyjádřit nějaký konkrétní případ (a to jsem zkusil), tak mi vyjde, že soustava nemá řešení.
Báze tedy musí vypadat jinak a to je to, na co se ptám.
Offline
#8 22. 10. 2016 16:13
Re: Příklad na vektorové prostory matic
↑ dominiksep: těch vektorů báze není m*n-1 ale m+n-1 a obecnou matici m*n z nich samozřejmě nevyjádříš, ale ten prostor taky neobsahuje všechny matice
Offline
#9 22. 10. 2016 16:49 — Editoval dominiksep (22. 10. 2016 16:51)
- dominiksep
- Příspěvky: 54
- Reputace: 0
Re: Příklad na vektorové prostory matic
↑ Stýv:
Jo, už mi to došlo, omlouvám se za svoji zabedněnost...
Teď jak to zapsat pro obecnou matici m*n. Můžu použít BÚNO a dokázat to třeba pro 3*3?
Nebo radši 2*2, matici o 9 řádcích nechci...
Offline
#11 22. 10. 2016 20:19
- dominiksep
- Příspěvky: 54
- Reputace: 0
Re: Příklad na vektorové prostory matic
↑ Stýv:
To jsem si říkal, ale nedovedu si představit, jak dokážu jejich lineární nezávislost a to, že generují V. U matice 2*2 jsem to řešil jako soustavu rovnic.
Offline

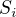 je matice s jedničkama v i-tém sloupci a nulama jinde, podobně
je matice s jedničkama v i-tém sloupci a nulama jinde, podobně 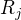 pro ty řádkové...
pro ty řádkové...