Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 11. 2016 20:05
- dominiksep
- Příspěvky: 54
- Reputace: 0
Definice suprema při sup M = +nekonečno
Ahoj,
chtěl bych se zeptat, zda mám správně přepsané výroky pro definici suprema množiny 
1) 
2) 
Úplně si nejsem jistý, co přesně mám napsat. Vlastně by stačilo jen napsat, že množina není shora omezená, ale v zadání vyloženě stojí napište, co je třeba ověřit, abychom z definice suprema dokázali vztah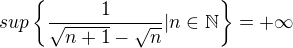
Proto jsem chtěl užít výroky uvedené v definici suprema.
Děkuji
Offline
#2 03. 11. 2016 20:39
Re: Definice suprema při sup M = +nekonečno
Ahoj ↑ dominiksep:,
Najprv urob tuto upravu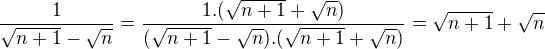
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 04. 11. 2016 10:07 — Editoval Rumburak (04. 11. 2016 14:41)
Re: Definice suprema při sup M = +nekonečno
↑ dominiksep:
Ahoj.
Ano, chápeš to správně, přesně v souladu s definicí suprema je potřeba ověřit platnost výroků, které jsi napsal.
V tomto případě se to ovšem poněkud zjednoduší:
Zkoumaná množina je podmnožinou množiny reálných čísel a je-li kandidátem na její supremum  , potom první
, potom první
z dokazovaných výroků je splněn triviálně. Takže "v praxi" pak už opravdu stačí podrobně dokázat pouze ten
druhý výrok, který de facto říká, že daná množina není shora omezená.
Kolega ↑ vanok:, kterého také zdravím, Ti naznačuje cestu k důkazu toho druhého výroku.
Offline
