Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 19. 11. 2016 23:40
- 126Magdaléna126

- Příspěvky: 30
- Reputace: 0
Pravdepodobnosť
Zdravím, neviem si dať rady s týmto
Dokáž, že ak m1, m2, m3 sú členy AP, tak  sú členy GP. Urč q.
sú členy GP. Urč q.
Offline
#3 20. 11. 2016 14:56
- 126Magdaléna126

- Příspěvky: 30
- Reputace: 0
Re: Pravdepodobnosť
↑ jarrro: áno,to som si vyjadrila..
Čiže mám :
m1
m2= m1 +d
m3= m1+2d
A ďalej ? :/
Zatiaľ ďakujem
Offline
#5 20. 11. 2016 15:47
- 126Magdaléna126

- Příspěvky: 30
- Reputace: 0
Re: Pravdepodobnosť
↑ misaH:
Takže takto? 
No a teraz vlastne porovnám tie exponenty? 
Offline
#7 20. 11. 2016 16:09
- 126Magdaléna126

- Příspěvky: 30
- Reputace: 0
Re: Pravdepodobnosť
↑ misaH:
Ahaa..ano, to mám...ďakujem..
A dalej? :/
Offline
#8 20. 11. 2016 16:25
- 126Magdaléna126

- Příspěvky: 30
- Reputace: 0
Re: Pravdepodobnosť
A vyšlo mi to vlastne, že
Správne zatiaľ? :/
Offline
#9 20. 11. 2016 17:31
- misaH
- Příspěvky: 13459
Re: Pravdepodobnosť
↑ 126Magdaléna126:
Tak ja myslím, že d je asi ľubovoľná diferencia.
Ty máš zistiť q.
Jarrro ti to všetko napísal...
Offline

 pomocou
pomocou 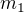 a
a 

 bude spoločná hodnota tých podielov
bude spoločná hodnota tých podielov