Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Distribuční funkce náhodné veličiny (TOTO TÉMA JE VYŘEŠENÉ)
#1 10. 02. 2017 18:00 — Editoval slender (10. 02. 2017 18:00)
Distribuční funkce náhodné veličiny
Ahoj,
snažím se vyřešit tuto úlohu:
Nechť 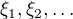 jsou nezávislé stejně rozdělené náhodné veličiny s rozdělením:
jsou nezávislé stejně rozdělené náhodné veličiny s rozdělením:![kopírovat do textarea $P[\xi=k]=\frac{1}{10}$](/mathtex/e7/e79998daa6013e99c74fc9730ee35817.gif) pro
pro 
Definujme náhodnou veličinu 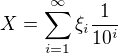 .
.
Určete distribuční funkci náhodné veličiny X.
Poradil by mi prosím někdo, jak začít?
Offline
- (téma jako vyřešené označil(a) slender)
#3 11. 02. 2017 14:37 — Editoval slender (11. 02. 2017 14:37)
Re: Distribuční funkce náhodné veličiny
↑ Stýv: Jediné na co jsem zatím přišel je, že pro zjištění rozdělení bych měl vycházet z věty o rozdělení součtu náhodných veličin:
Pro součet diskrétních náhodných veličin  platí:
platí:![kopírovat do textarea $P[Z=z]=\sum_{x}{P[X=x,Y=z-x]}$](/mathtex/2a/2a97a66094657a3b3515877f30f62d8e.gif)
Nevím ale, jak ji přesně využít u nekonečného součtu, když jsou navíc náhodné veličiny násobeny 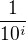 .
.
Offline
#5 11. 02. 2017 15:05
Re: Distribuční funkce náhodné veličiny
↑ slender: obvykle se píše [0,1], ale jinak je to dobrý začátek. pokud nemáš představu, o jaké konkrétní rozdělení na intervalu [0,1] se jedná, zkus si určit třeba P(X<=0,374)
Offline
#6 11. 02. 2017 15:27 — Editoval slender (11. 02. 2017 15:47)
Re: Distribuční funkce náhodné veličiny
↑ Stýv: Díky, zatím jsem dospěl jen k tomuhle:![kopírovat do textarea $P[X\leq x]=P[\xi_1<x_1]+P[\xi_1=x_1,\xi_2<x_2]+P[\xi_1=x_1,\xi_2=x_2,\xi_3<x_3]+\dots$](/mathtex/3b/3ba697c57f6e41337c05fae2b1f2cff0.gif) kde jako
kde jako 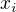 značím
značím  -té desetinné místo
-té desetinné místo  .
.
Šlo by to tedy ještě přepsat následovně, abych se zbavil 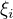 :
:
(edit, napsal jsem to špatně)![kopírovat do textarea $P[X\leq x]=\frac{x_1}{10}+\frac{x_2}{10^2}+\dots=\sum_{i=1}^{\infty}\frac{x_i}{10^i}$](/mathtex/23/23ded2d02f12601f00242436ad766a5f.gif)
Teď pro změnu přemýšlím nad tím, jak vyjádřit  -té desetinné místo
-té desetinné místo  rozumněji, než
rozumněji, než 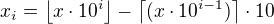 .
.
Offline
#7 11. 02. 2017 15:41 Příspěvek uživatele slender byl skryt uživatelem slender. Důvod: Napsal jsem tam nesmysl.
#10 11. 02. 2017 16:07
Re: Distribuční funkce náhodné veličiny
↑ slender: no to zase prrr! ![kopírovat do textarea $P[X\leq x]=x$](/mathtex/f2/f27f9ca5e657c8463b3aefc996f8f5be.gif) je správně, ale to přece není hustota
je správně, ale to přece není hustota
Offline
#11 11. 02. 2017 16:08 — Editoval Jj (11. 02. 2017 16:09) Příspěvek uživatele Jj byl skryt uživatelem Jj. Důvod: Není nutné.
#13 11. 02. 2017 16:35
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Distribuční funkce náhodné veličiny (TOTO TÉMA JE VYŘEŠENÉ)

 tvoří
tvoří ![kopírovat do textarea $[0,0.\overline{9}]$](/mathtex/d0/d04ea6052cdf5caa1ae48ef1fa6c4f50.gif) .
.![kopírovat do textarea $\int_{-\infty}^x f(u)\mathop{}\!\mathrm{d}u=0+\int_0^{x}u \mathop{}\!\mathrm{d}u=\left[\frac{u^2}{2}\right]_0^x=\frac{x^2}{2}$](/mathtex/ec/ecbd5ce7c3fafb60443d621f95b3feb7.gif)
 , že?
, že?