Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 13. 06. 2009 11:59 — Editoval Kessi (13. 06. 2009 12:01)
Rozklad součinu podle vzorců
Ahoj, pozítří mám velkou zkoušku a sešit jsem si nechala ve škole. Nutně bych potřebovala vědět jaké jsou vzorce na rozklad a kdyby jste byl někdo tak hodný a i mi to vysvětlil moc by mi to pomohlo pro příklad sem dám nějaký příklad, který jsem našla na internetu. Stačilo by mi po lopatě vysvětlit jak se to má počítat, já jsem prostě úplně mimo.
Ještě jednou moc děkuji.
Offline
#5 14. 06. 2009 09:50 — Editoval matoxy (14. 06. 2009 10:41)
Re: Rozklad součinu podle vzorců
You know who
(or maybe not)
Offline
#6 14. 06. 2009 09:52 — Editoval Redvo (14. 06. 2009 10:02)
Re: Rozklad součinu podle vzorců

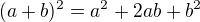
a zdá sa mi že aj takto ešte, to je to isté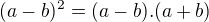
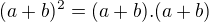
↑ matoxy: máš tam preklep, miesto - si dal / :)
a si si istý že 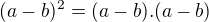 ? mne sa zdá že
? mne sa zdá že 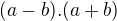
takže je to určite tak jak som hovoril ja, matoxy sa asi pomýlil, spravil som si skúšku...
Matematika je jemná a citlivá dohoda o tom že 2+2=4 ;)
Offline
#8 14. 06. 2009 10:18
Re: Rozklad součinu podle vzorců
↑ halogan: nemôžeš niekedy napísať niečo konkrétne? :D
Matematika je jemná a citlivá dohoda o tom že 2+2=4 ;)
Offline
#9 14. 06. 2009 10:39
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Rozklad součinu podle vzorců
↑ halogan:
Já bych byla opatrná - myslím, že množina jablek není uzavřena na násobení nebo jak se tomu chytře říká (raděj bych se poptala u odborníků - zemědělců nebo lesáků, třeba). Jinak model jablek řeším tady
↑ Redvo:
Kolega halogan chtěl naznačít, že (5-2)(5-2) není totež jako (5-2)(5+2)
OT: Já mám zas velkou a troufalou prosbu - nemůžeš trochu pozměnit podpis? - já, třeba určitě jsem na tom "horšie", ale je nutné mi to pořad připomínat? Pravda, podpis je velmi soukromá věc, rozumím, pokud tu prosbu nebudeš nijak akceptovat, omlouvám se (chtěla jsem o to poprosit mailem, ale nemas v profilu, tak musim takto). Děkuji.
Offline
#12 14. 06. 2009 10:52
Re: Rozklad součinu podle vzorců
↑ jelena: podpis bola len taká moja myšlienka čo ma raz napadla asi pred týždňom, pretože ja už mám dosť ako mi veštci okolo hovoria že koľko toho viem, že som múdry atď..tak som si len toto pomyslel :) Pochybujem že ty si jedna z tých čo ma ospevuje ako múdreho keď vlastne dokazujem že nič neviem :D tak ja to teda zmením..a doplním si kontaktné údaje keby si ma chcela niekedy kontaktovať :)
Matematika je jemná a citlivá dohoda o tom že 2+2=4 ;)
Offline
#13 14. 06. 2009 11:04
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Rozklad součinu podle vzorců
↑ Redvo:
Toto se mi libilo velmi moc, děkuji :-)
Offline
#14 14. 06. 2009 12:05 — Editoval Redvo (14. 06. 2009 12:08)
Re: Rozklad součinu podle vzorců
↑ jelena: no tak to potešilo aj mňa že som to mal správne, najprv som si bol istý na 100% ale keď napísal ttopi niečo iné tak som nejako stratil istotu..aspoň už viem že keď som si niečim istý tak si to mám obhájiť a nie sa len ospravedlňovať jak splašené kura keď viem že to mám dobre :)
PS: veľmi ďakujem za pochvalu, ani nevieš ako ma to potešilo :-*
Matematika je jemná a citlivá dohoda o tom že 2+2=4 ;)
Offline
#15 20. 02. 2011 15:25
- marekjakub

- Zelenáč
- Příspěvky: 20
- Reputace: 0
Re: Rozklad součinu podle vzorců
chtěl bych se zeptat zda mam dobře určené kořeny
x na druhou -8x + 32=0
kořen me vyšel x1=4
x2=8
předem děkuji za odpověď.
Offline
#16 20. 02. 2011 15:26
- Dana1
- Host
Re: Rozklad součinu podle vzorců
↑ marekjakub:
Založ si novú tému, kde si sa tu vzal?
Stačí, keď urobíš skúšku dosadením. Najprv všade číslo 4 a potom číslo 8.
 v tomto případě je:
v tomto případě je: