Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 14. 04. 2017 11:06
Cantelliho veta
zdravim
zaujimal by ma co najintuitivnejsi pohlad na Cantelliho (Borelovu vetu)
mame teda
Cantelli
Nech  je postupnost nahodnych javov a nech
je postupnost nahodnych javov a nech  . Potom
. Potom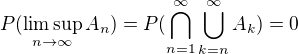
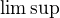 ma znazornovat, ze nastalo nekonecne vela javov
ma znazornovat, ze nastalo nekonecne vela javov 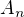
preco je tomu tak ? ako sa da nahliadnut, ze prave tato mnozinova operacia nam vravi toto ?
Dakujem
Per aspera ad astra
Offline
#2 14. 04. 2017 12:40
Re: Cantelliho veta
Povedať, že  patrí do nekonečne veľa prvkov množinovej postupnosti je to isté ako povedať, že nie je pravda, že
patrí do nekonečne veľa prvkov množinovej postupnosti je to isté ako povedať, že nie je pravda, že  patrí iba do konečne veľa prvkov tej postupnosti.
patrí iba do konečne veľa prvkov tej postupnosti.
Teda 
Ale ak patri iba do konečne veľa
patri iba do konečne veľa  , tak existuje
, tak existuje  také že
také že  nepatrí do
nepatrí do  pre k väčšie najviac rovné n.
pre k väčšie najviac rovné n.
Teda 
Teda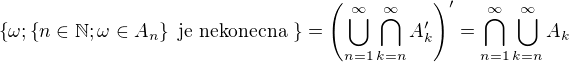
MATH IS THE BEST!!!
Offline
#3 14. 04. 2017 18:16 — Editoval vytautas (14. 04. 2017 18:43)
Re: Cantelliho veta
Ak chapem spravne, tak ak  , tak
, tak  take, ze
take, ze 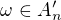
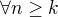 , teda
, teda 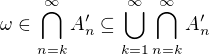 Teda mam, ze
Teda mam, ze  Ako viem, ze
Ako viem, ze 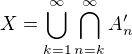 ?
?
Dakujem.
Edit 1:
Nam nejde o to, aby 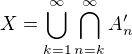 , ze ?
, ze ?
Ak  co je jav, ze
co je jav, ze  je len v konecnom pocet mnozin (nastal konecny pocet javov) , tak my chceme presny opak, aby
je len v konecnom pocet mnozin (nastal konecny pocet javov) , tak my chceme presny opak, aby 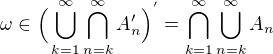 , teda nastalo nekonecne vela javov. Je to tak ?
, teda nastalo nekonecne vela javov. Je to tak ?
Edit 2:
Teda podobne plati aj pre  , nie ? Ked si zoberiem
, nie ? Ked si zoberiem  , teda patri do vsetkych az na konecny pocet, tak mam, ze existuje
, teda patri do vsetkych az na konecny pocet, tak mam, ze existuje 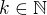 take, ze
take, ze 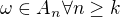 , teda
, teda 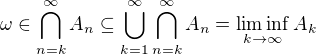 .
.
Mam pravdu ?
Per aspera ad astra
Offline