Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 15. 04. 2017 17:40
Pravdivost formule
Zdravím, řeším tuto úlohu a nevím, jestli mé řešení je správné:
Tablo metodou rozhodněte, zda je následující tvrzení pravdivé: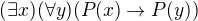
Tablo jsem udělal následující:
Předpokládám, že protože se mi podařilo vyvrátit negaci tvrzení, tak je tvrzení pravdivé?
Offline
#2 19. 04. 2017 18:05
Re: Pravdivost formule
↑ slender:
Ahoj. Řekl bych, že výsledek bude záviset na predikátu P.
Zkus vyšetřit dva případy :
I. P(x) neplatí ,
II. P(x) platí.
Offline
#3 19. 04. 2017 20:26
Re: Pravdivost formule
↑ Rumburak:ahoj . síce tablo metóde nerozumiem , ale tvrdenie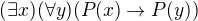 je pravdivé pre každý výrok P, lebo buď
je pravdivé pre každý výrok P, lebo buď 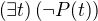 a stačí položiť
a stačí položiť 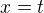 alebo
alebo 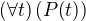 a teda platí dokonca
a teda platí dokonca 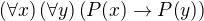
Či mi niečo ušlo?
MATH IS THE BEST!!!
Offline
